Question

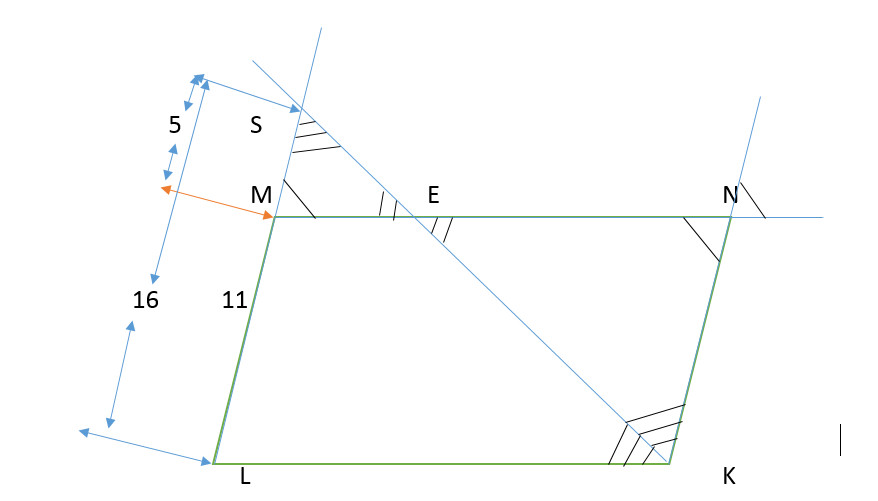
в параллелограмме KLMN проведена биссектриса угла K которая пересекает продолжение стороны LM в точке S;LS=16,MS=5 найдите периметр параллелограмма KLMN

Answer 1

если s продолжение и MS=6, а LS=16, тогда LM=16-5=11 и NK=11 , тк они равны.
далее получаем, что угол LKS=углуKSL, тк угол KSL=углуNKS, а угол NKS=углуKSL(ПОТОМУ ЧТО ОНИ НАКРЕСТ ЛЕЖАЩИЕ УГЛЫ ПРИ СЕКУЩЕЙ KS И ПРЯМЫХ LS и KN) тогда отрезок KS-основание равнобедренного треугольника KSL(углы у основания равны)? следовательно LS=LK=16, следовательно и MN тоже равен 16
получаем P=11+11+16+16=54

Answer 2

Рассмотрим углы в треугольниках MSE и EKM :
углы при вершине Е равны  
два угла при вершине N равны углу при вершине M
два угла при вершине К равны углу при вершине S
т.е. углы    MSE и EKM равны , из чего следует что
треугольник KLS равнобедренный и стороны LS=LK =16.
LK и LM являются сторонами параллелограмма :
LM = LS-MS =16-5=11
LK=16 периметр параллелограмма KLMN:
P=2*(11+16)=54
Смотри рисунок.