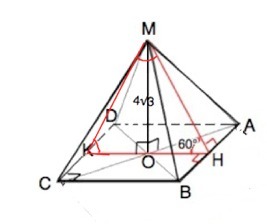
в правильной четырёхугольной пирамиде высота равна 4 корня из 3, а двугранный угол при основании равен 60 градусов. найдите площадь полной поверхности пирамиды.
Ответы
В основании правильной четырехугольной пирамиды - квадрат.
Величина двугранного угла при основании пирамиды измеряется его линейным углом. Он составлен двумя отрезками, проведенными перпендикулярно ребру основания в одной точке, т.е. углом между апофемой МН и отрезком КН, проведенным параллельно ВС и, следовательно, перпендикулярным АВ, так как основание - квадрат.
Так как угол МНК=60°, а апофемы равны, ∆ КМН - равносторонний.
Высота МО перпендикулярна плоскости основания, следовательно, перпендикулярна КН.
Из прямоугольного ∆ МОН апофема МН=МО:sin60°=8 (ед.длины).
СВ║КН и равна ей.
Стороны основания равны 8 (ед. длины).
Площадь полной поверхности пирамиды равна сумме площадей основания и боковой поверхности.
S осн=АВ²=64 (ед. площади)
S бок=4S MAB=4•МН•AB:2
S бок=4•8•8:2=128 (ед. площади)
S полн==64+128= 192 (ед. площади)