Question

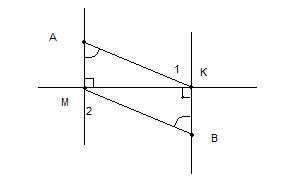
Точки А и В лежат по разные стороны от прямой,АМ и ВК -перпендикуляры к этой прямой .Докажите что треугольник АМК равен треугольнику ВКМ ,если угол МАК равен углу МВК

Answer 1

Две прямые, перпендикулярные к третьей, не пересекаются, значит AMIIBK.
<1=<MAK как накрест лежащие углы при пересечении двух параллельных прямых АМ и ВК секущей АК. Значит
<AKM=90-<1=90-<MAK
<2=<MBK как накрест лежащие углы при пересечении двух параллельных прямых АМ и ВК секущей ВМ. Значит
<BMK=90-<2=90-<MBK 
По условию <MAK=<MBK, значит <AKM=<BMK
Прямоугольные треугольники АМК и ВКМ равны, таким образом, по катету и прилежащему к нему острому углу: катет МК - общий, острые углы АКМ и ВМК равны.