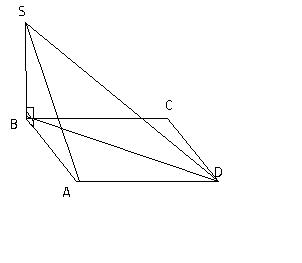
1.до площини квадрата abcd проведено перпендикуляр sb,sb=12 см.Знайдіть площу триугольника sad,якщо ab=5см.
Ответы
Не очень силен в украинском, поэтому напишу решение на русском.
SB перпендикулярно плоскости ABCD, значит перпендикулярно любой линии, лежащей в этой плоскости, в том числе и AB и BC. Значит треугольник SBA - прямоугольный.
По теореме Пифагора:
SA^2 = AB^2 + BS^2
SA^2 = 25 + 144 = 169
SA = 13
Проведем диагональ BD
Диагональ квадрата со стороной а равна а*корень2
BD = 5*корень2
BD так же лежит в плоскости ABCD следовательно SB перпендикулярно BD, следовательно треугольник SBD прямоугольный.
SD^2 = BD^2 + BS^2
SD^2 = 50 + 144 = 194
SD = корень194
По формуле Герона:
S^2 = p(p-a)(p-b)(p-c) где p - половина периметра треугольника, abc - стороны
p = (18+корень194)/2
S^2 = ((18+корень194)/2)*((18+корень194)/2 - корень194)*((18+корень194)/2 - 5)*((18+корень194)/2 - 13) = ((18+корень194)/2)*((18 - корень194)/2)*((корень194 - 8)/2)*((корень194+8)/2) = ((18^2 - (корень194)^2)/4)*(((корень194)^2 - 8^2)/4)= ((324-194)/4)*((194-64)/4) = (130/4)*(130/4) = 1056,25
S^2 = 1056,25
S = 32,5 см^2
Ответ: 32,5 см^2
Капец же