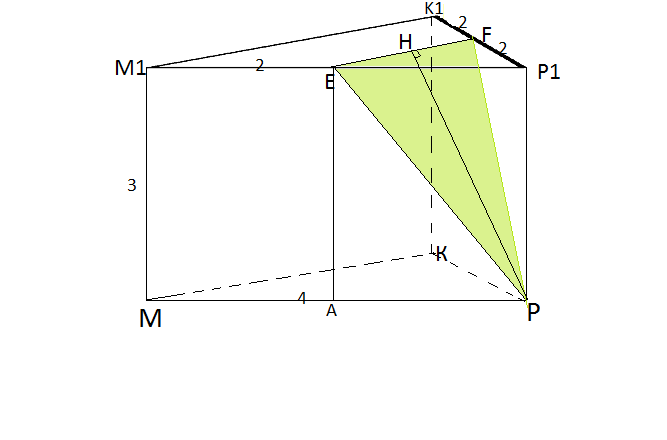
MKPM1K1P1 — правильная треугольная призма, сторона основания которой 4 см. Найдите площадь сечения призмы плоскостью, проходящей через точки Р, Е и F, где Е и F — середины ребер M1P1 и К1Р1, а боковое ребро равно 3 см.
Ответы
Площадь пересечения плоскости с призмой равна площади треугольника ЕFP.
Площадь ΔЕFP = ½PH*EF
Найдем значение EF.
ΔЕР₁F подобен Δ M₁K₁P₁.
Все стороны ΔM₁K₁P₁ равны 4. При этом ЕР₁=½М₁Р₁=2 см.
⇒ все стороны ΔЕР₁F равны 2 : FP₁=EP₁=EF=2 см
EF=2
Найдем значение PH.
Из ΔЕАР выразим значение EP:
EP²=EA²+AP²
Так как боковое ребро правильной призмы равно 3, то ЕА=ММ₁=3 см
АР=МР/2 = 2 , где МР=4 см - сторона основания призмы.
EP²=9+4=13 см²
Из ΔЕРН выразим РН:
РН²=ЕР²-ЕН²=13-1=12 см²
PH=2√3 см
Посчитаем площадь ΔЕРF:
S ΔEPF = ½PH*EF= ½ * 2√3 * 2= 2√3 см²
Ответ. Площадь пересечения призмы с плоскостью EFP равна 2√3 см²