Предмет: Геометрия,
автор: azarnov1998
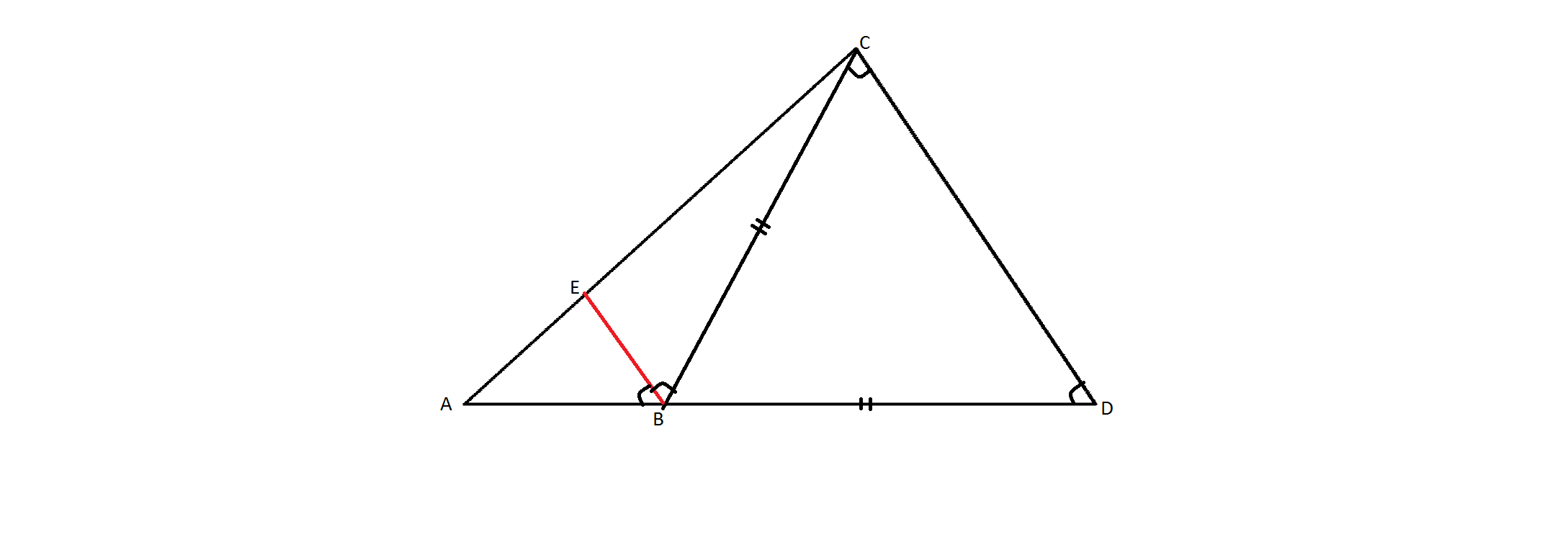
помогите решить задачу по геометрии:дан треугольник DAC на стороне DA отложена точка B так что DB=BC,угол В= углу C. Из угла ABC проведена биссектриса BE. Доказать , что DC параллельна BE
Ответы
Автор ответа:
0
Сумма углов треугольника равна 180°. ⇒ угол ВДС+ угол ВСД + угол ДВС = 180°
При этом угол ВДС= углу ВСД = α
⇒ угол ДВС=180-2α
Угол ДВА - развернутый и равен 180°. При этом угол ДВА=угол ДВС+угол АВС
180=180-2α+ угол АВС
⇒угол АВС = 2α
ВЕ - биссектриса угла АВС. ⇒ угол АВЕ=углу ЕВА= α
По теореме:
Если две параллельные прямые пересечены третьей прямой, то внутренние накрест лежащие углы равны.
У нас угол ЕВС=углу ВСД откуда следует, что ВЕ параллельна ДС.
Приложения:
Похожие вопросы
Предмет: Геометрия,
автор: 1000вопросов
Предмет: Информатика,
автор: ayechkaazamatova
Предмет: Русский язык,
автор: Ivsnoklopgolgmailcom
Предмет: Математика,
автор: GulfizaGibadullina
Предмет: Математика,
автор: Школьнмца