Предмет: Математика,
автор: Kwantowa
Терміново!!!№2,будь ласка!!
Приложения:
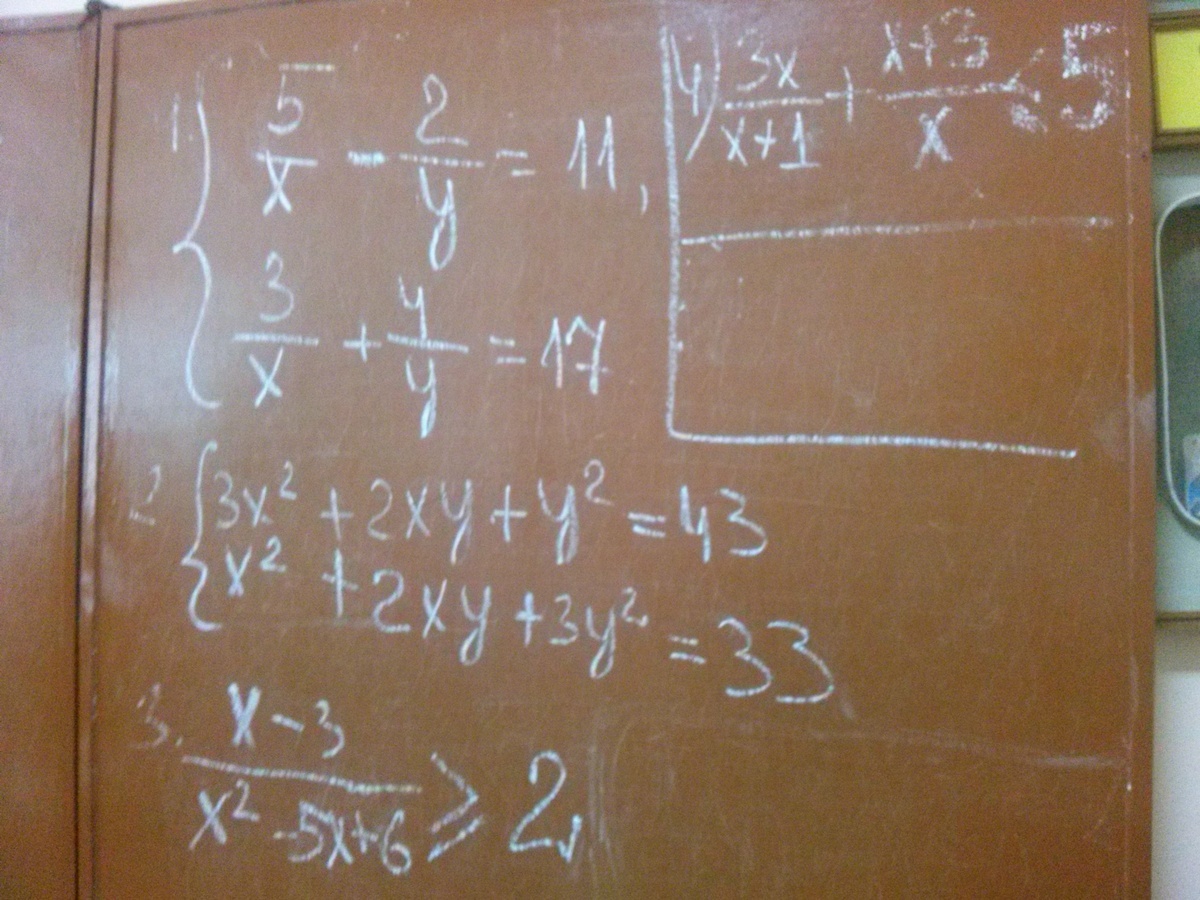
Ответы
Автор ответа:
0
можно вычесть из первого уравнения второе: 2(x^2 - y^2) = 10
x^2 = 5 + y^2
----------------
из второго получим: 5 + y^2 + 2xy + 3y^2 = 33
2xy = 28 - 4y^2
xy = 14 - 2y^2
x = 14/y - 2y
подставим...
(14/y)^2 - 56 + 4y^2 = 5 + y^2
196/y^2 - 61 + 3y^2 = 0
биквадратное уравнение...
3(y^2)^2 - 61(y^2) + 196 = 0
D = 61*61 - 4*3*196 = 37^2
(y^2) = (61-37)/6 или (y^2) = (61+37)/6
(y^2) = 4 или (y^2) = 49/3 _____ x^2 = 9 или x^2 = 64/3
y = +-2 _____ x = +-3
y = +-7/V3 = +-7V3 / 3 _____ x = +-8/V3 = +-8V3 / 3
надеюсь, я нигде не ошиблась...
x^2 = 5 + y^2
----------------
из второго получим: 5 + y^2 + 2xy + 3y^2 = 33
2xy = 28 - 4y^2
xy = 14 - 2y^2
x = 14/y - 2y
подставим...
(14/y)^2 - 56 + 4y^2 = 5 + y^2
196/y^2 - 61 + 3y^2 = 0
биквадратное уравнение...
3(y^2)^2 - 61(y^2) + 196 = 0
D = 61*61 - 4*3*196 = 37^2
(y^2) = (61-37)/6 или (y^2) = (61+37)/6
(y^2) = 4 или (y^2) = 49/3 _____ x^2 = 9 или x^2 = 64/3
y = +-2 _____ x = +-3
y = +-7/V3 = +-7V3 / 3 _____ x = +-8/V3 = +-8V3 / 3
надеюсь, я нигде не ошиблась...
Автор ответа:
0
дуже-дуже тобі вдячна!!!
Ти мене справді виручила)
Ти мене справді виручила)
Похожие вопросы
Предмет: Қазақ тiлi,
автор: kazimirmensadirov205
Предмет: Математика,
автор: tatyana070709
Предмет: Окружающий мир,
автор: sofiacvetkova33
Предмет: Математика,
автор: Ivanka13