Question

 Постройте касательную к данной окружности проходящую через данную точку  этой окружности. ( пожалуйста чертёж) 

Answer 1

Нам дана окружность, значит известен ее центр.
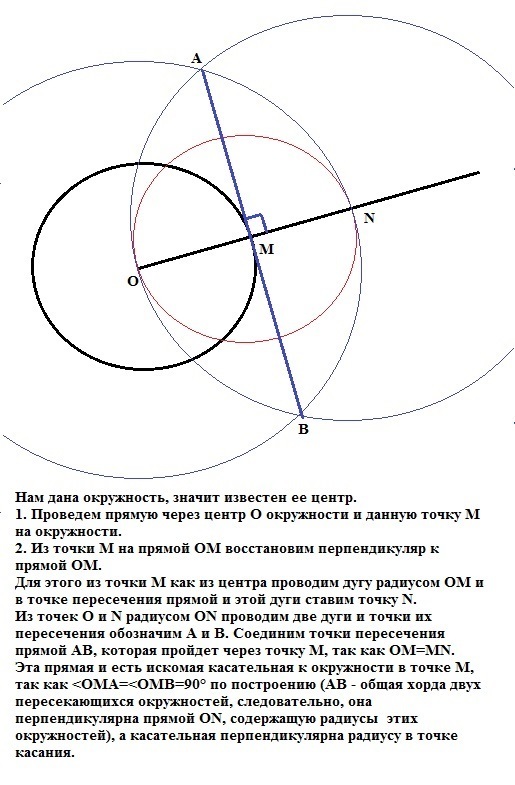
1. Проведем прямую через центр О окружности и данную точку М на окружности.
2. Из точки М на прямой ОМ восстановим перпендикуляр к прямой ОМ.
Для этого из точки М как из центра проводим дугу радиусом ОМ и в точке пересечения прямой и этой дуги ставим точку N. Из точек О и N радиусом ОN проводим две дуги и точки их пересечения обозначим
А и В. Соединим точки пересечения прямой АВ, которая пройдет через точку М, так как ОМ=MN. эта прямая и есть искомая касательная к окружности в точке М, так как <OMA=<OMB=90° по построению, а касательная перпендикулярна радиусу в точке касания.