Question

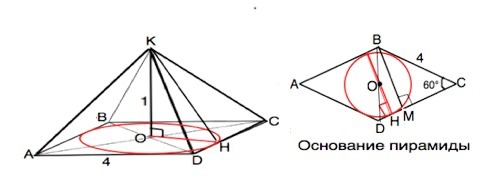
KABCD- Четырехугольная пирамида, ABCD- ромб, AB=BD, P(ABCD)=16, КО перпендикуляр (АВС), КО=1 Найти: Sбок

Answer 1

Ромб, меньшая диагональ которого равна боковой стороне, состоит из 2-х равносторонних треугольников. 

 КО - перпендикуляр к плоскости ромба, О - точка пересечения его диагоналей и центр вписанной окружности.

Высоты боковых граней равны.  

Диаметр вписанной в ромб окружности равен высоте ромба. 

Каждая сторона ромба 16:4=4.

В ∆СBD угол ВСD=60°, тогда высота 

ВМ=ВС•sin60°=2√3

OH=r=√3

Высота КН боковой грани из ∆ КОН по т.Пифагора 

КН=√(KO²+OH²)=√(1+3)=2

Sбок=4•S ∆ KCD

S ∆ KCD=KH•CD:2=2•4:2=4 

S бок=4•4=16 (ед. площади)