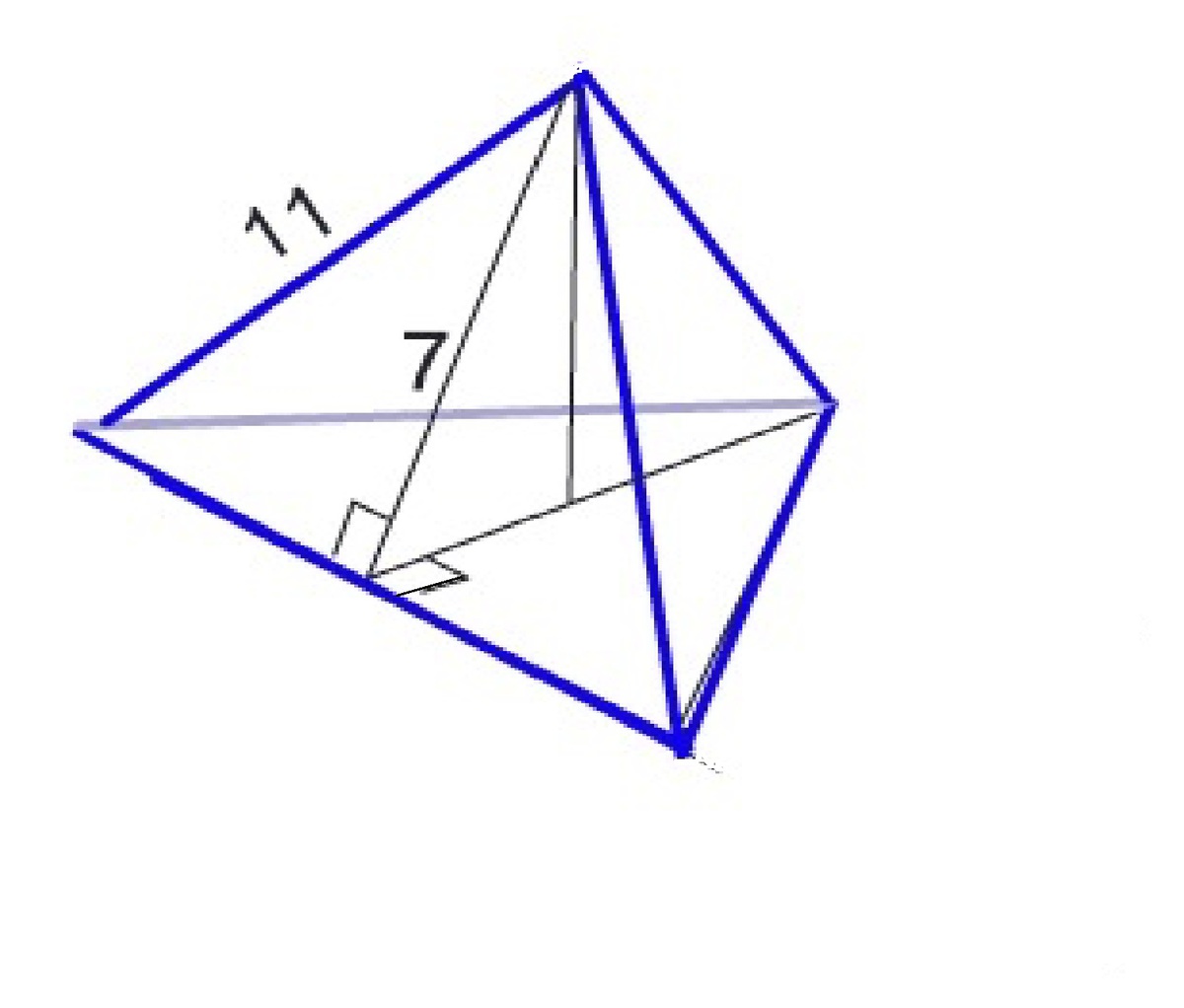
боковое ребро и апофема правильной треугольной пирамиды соответственно равны 11 см и 7 см. Вычислить площадь сечения, проходящего через боковое ребро, и высоту пирамиды
Ответы
Искомая площадь равна половине произведения высоты пирамиды на основание треугольника со сторонами апофема, ребро, и основанием - высота треугольника в основании.
Половину стороны основания найдем по теореме Пифагора.
х= √(11²-7²)=√121-49=6√2
Cторона основания равна
2*6√2=12√2
Высота правильного треугольника h равна
h=а√3:2=12√2*√3:2=6√6
Основание высоты пирамиды находится на расстоянии 1/3 от основания апофемы, так как центр ее - на пересечении медиан ( они пересекаются в отношении 2:1 от вершины) и это расстояние равно 2√6
Найдем высоту пирамиды.
h=√49-24=√25=5
Площадь сечения
S=(5*6√6):2=15√6 см²