Question

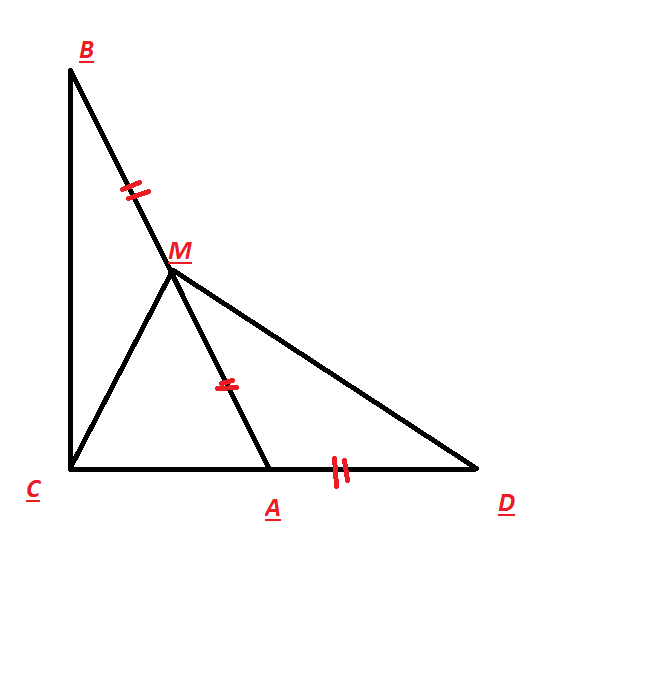
В прямоугольном треугольнике АВС угол С = 90 градусов, угол А - в 2 раза меньше от угла В, катет АС - продолжено на отрезок AD так что AD = 1/2 (одна вторая) АВ. Найти ВС, если DC = 15 cм.

Answer 1

Пусть угол A=x, тогда угол B=x/2. Сумма угол в треугольнике равна 180'. 
x+(x/2)+90'=180'. x=60', т.е. угол A=60', тогда угол B=30'. CA=BA/2=MA.
Рассмотрим треугольник CMA. 
Угол MAC=60', т.к. CA=AM, тогда угол AMC=углу ACM =60'. 
Таким образом, треугольник AMC-равносторонний. MA=CA=CM. 

Т.к. угол BAC=60', тогда угол BAD=120' (как смежные).

Точку M соединим с точкой D. 
Рассмотрим треугольник MAD. MA=AD, угол AMD=углу MAD=30'. 
Рассмотрим треугольник CMD. Угол CMD=90' (180-угол MCD-угол CDM=180-60-30=90'). В треугольнике CMD: CD=15, тогда CM=7,5 (против угла в 30'). 
Но CM=MA. A MA является половиной AB. Следовательно, AB=2MA=2*7,5=15. 

Тогда по т. Пифагора: BC^2=AB^2-CA^2. BC= $7,5 sqrt{3}$