Предмет: Алгебра,
автор: Аноним
знатоки алгебры сюда!
Приложения:
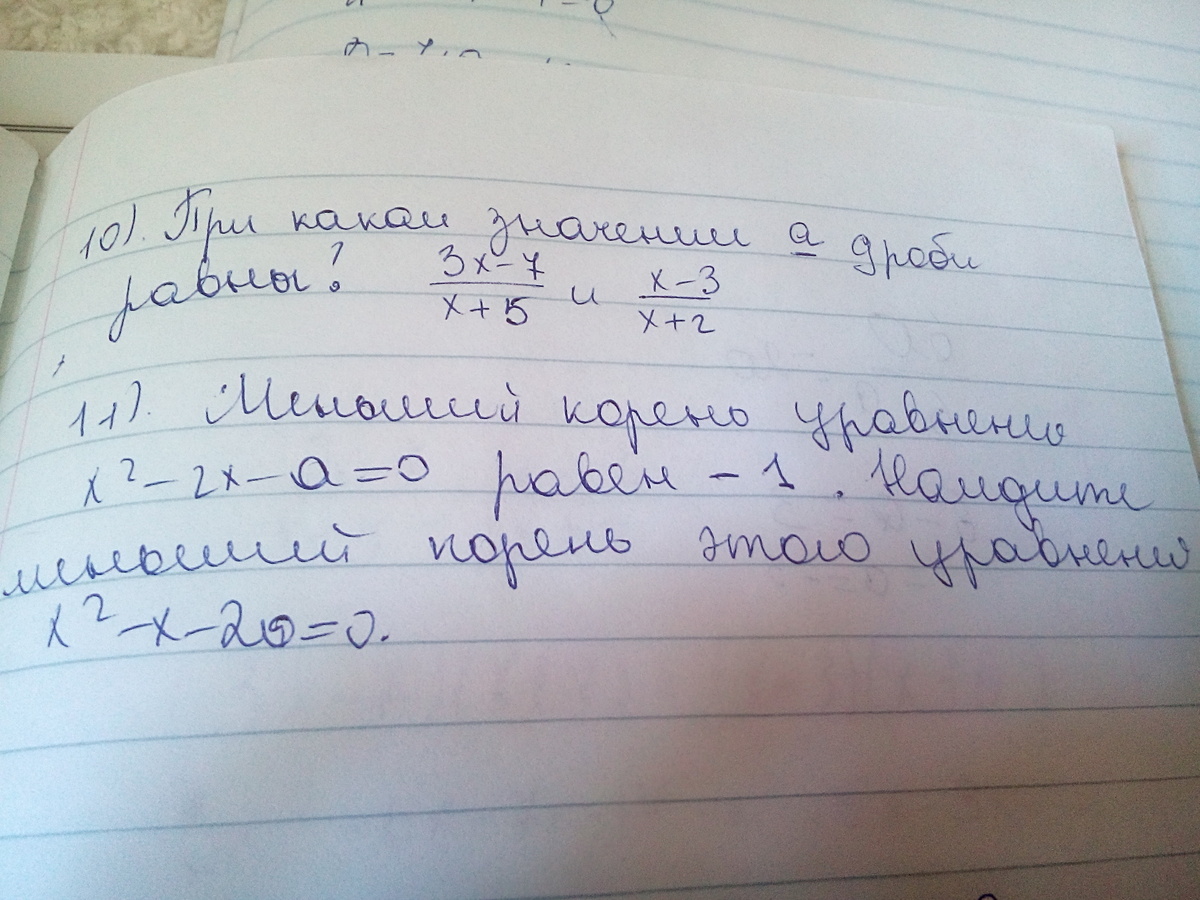
Ответы
Автор ответа:
0
10)


11)
теорема Виетта

11)
теорема Виетта
Автор ответа:
0
====================================================
Приложения:

Похожие вопросы
Предмет: Физика,
автор: poljo162
Предмет: Математика,
автор: mariyabel
Предмет: Қазақ тiлi,
автор: aldiyarshaimerdenov1
Предмет: Математика,
автор: nedenispolybomy
Предмет: Геометрия,
автор: Vad1k0071