Предмет: Алгебра,
автор: Тоня0304
Вычислите предел числовой последовательности:
Приложения:
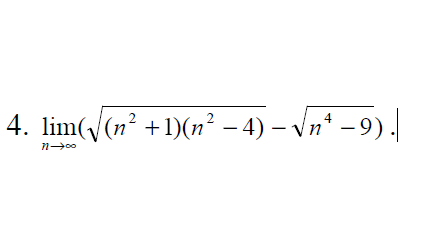
Ответы
Автор ответа:
0
первый корень в выражении обозначим кор1, второй корень за кор2, знак предела в переходах опустим за муторностью его писанины.
Исходное выражение домножим на сопряженное:
(кор1-кор2)*(кор1+кор2)/(кор1+кор2)=(n^4-3n^2-4-n^4+9)/(кор1+кор2)=


устремим n к бесконечности, получим:
=-3/2
Исходное выражение домножим на сопряженное:
(кор1-кор2)*(кор1+кор2)/(кор1+кор2)=(n^4-3n^2-4-n^4+9)/(кор1+кор2)=
устремим n к бесконечности, получим:
=-3/2
Автор ответа:
0
Cgfcb,J)
Автор ответа:
0
Спасибо)
Похожие вопросы
Предмет: Русский язык,
автор: kalibekkyzy09
Предмет: Математика,
автор: Аноним
Предмет: Алгебра,
автор: nazik181207
Предмет: Алгебра,
автор: Нюта1000
Предмет: Литература,
автор: НезнайкаЗайка