Предмет: Математика,
автор: Esavkina
НАПИШИТЕ УРАВНЕНИЕ КАСАТЕЛЬНОЙ К ГРАФИКУ ФУНКЦИИ
Приложения:
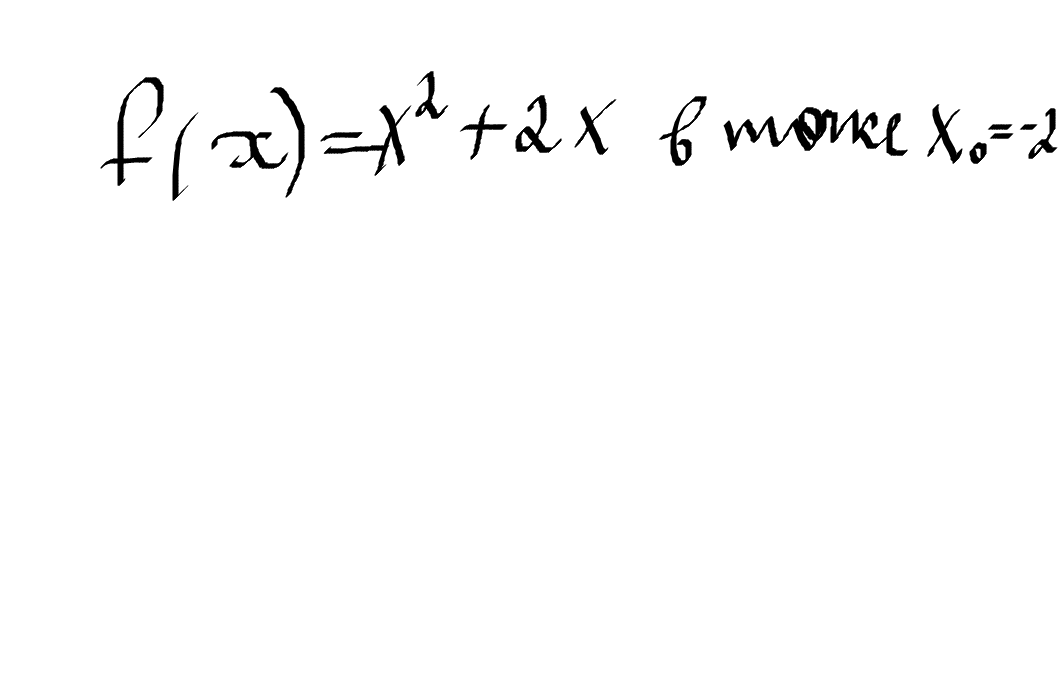
Ответы
Автор ответа:
0
Уравнение касательной: y = f ’(x0) * (x − x0)
+ f(x0). Точка x0 = -2 f (x0) и
f ’(x0) надо вычислить. Для начала найдем значение функции. f (x0) = f (-2) = (-2)²+2*(-2) = 4-4 = 0;
Теперь найдем производную: f ’(x) = (x²+2x)’ = 2x+2;
Подставляем в производную x0 = -2: f ’(x0) = f ’(-2) = 2*(-2)+2 = -2;
Итого получаем: y = -2 * (x −(-2) + 0 = -2x + 2.
Это и есть уравнение касательной.
f ’(x0) надо вычислить. Для начала найдем значение функции. f (x0) = f (-2) = (-2)²+2*(-2) = 4-4 = 0;
Теперь найдем производную: f ’(x) = (x²+2x)’ = 2x+2;
Подставляем в производную x0 = -2: f ’(x0) = f ’(-2) = 2*(-2)+2 = -2;
Итого получаем: y = -2 * (x −(-2) + 0 = -2x + 2.
Это и есть уравнение касательной.
Автор ответа:
0
Похожие вопросы
Предмет: Другие предметы,
автор: zhenis20100805
Предмет: Қазақ тiлi,
автор: orazalina2
Предмет: Алгебра,
автор: vettapuskareva
Предмет: Химия,
автор: MaratZy