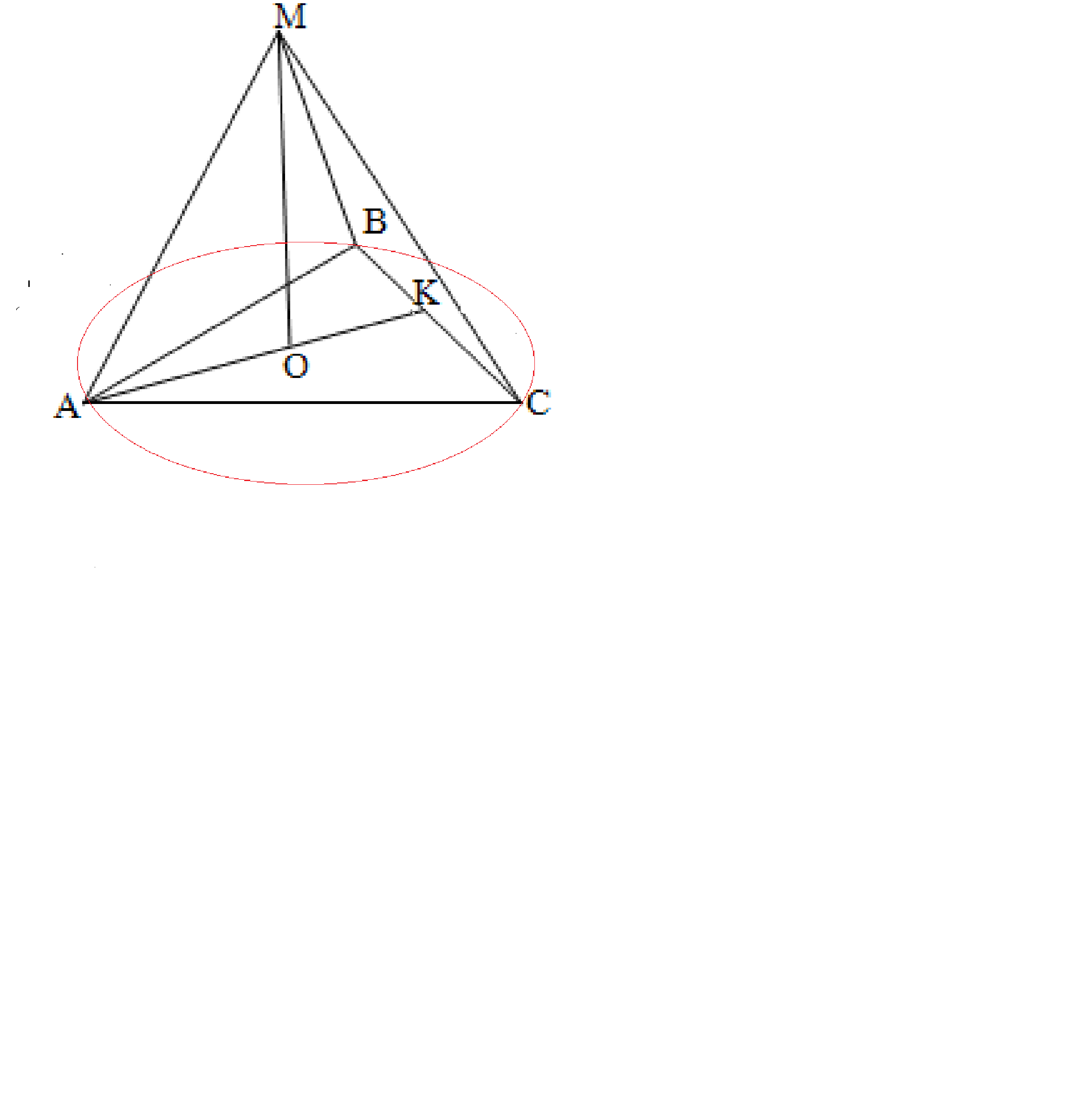
Дано Треугольную Пирамиду у которой все стороны равны 11
Нужно найти:
1)Площадь ( S )
2)Объем( V )
3) Площадь боковой поверхности (Sб.п.)
4)Площадь полной поверхности( Sп.п.)
СДЕЛАЙТЕ ОЧЕНЬ СРОЧНО!!!!!!!!Ответы
Треугольная пирамида, у которой ребра равны, является правильной. Все её грани являются равносторонними треугольниками.
1)Площадь ( S )
Надо понимать, площадь одной грани:
S=а²√3:4=121√3:4см²
3) Площадь боковой поверхности (Sб.п.)
Состоит из трех граней и равна
3 S=3 а²√3:4=363√3:4см²
4)Площадь полной поверхности( Sп.п.) - площадь всех четырех граней
4S=4 а²√3:4=а²√3=121√3 см²
2)Объем( V )
V=SH:3
Для того, чтобы вычислить объем, следует найти высоту H пирамиды.
Ее найдем из прямоугольного треугольника МАО, в котором
АМ- гипотенуза (ребро пирамиды)
МО( высота) - катет,
АО ( часть высоты основания) - катет
В правильной треугольной пирамиде основание её высоты находится в центре основания пирамиды, который одновременно является центром описанной окружности, поэтому
АО равна радиусу описанной окружности и равна 2/3 высоты основания.
Высота основания
h=а√3):2=11√3):2
R=2/3h= а√3):3=11√3):3
ОА=R=11√3):3
Найдем высоту пирамиды ОМ из треугольника АОМ:
ОM²=AМ²-OА²
ОM²=11²-{11√3):3} ²=121-121*3:9=(1089-363):9=726/9=242/3
ОМ=√(242/3)=11√2):√3
V = 1/3 Sh =1/3*{121√3:4}{11√2):√3}=1331√2:12 см³
---------------
Для объема правильного тетраэдра есть формула, которая позволяет пропустить все эти промежуточные вычисления:
V =а³√2):12
и тогда
V =11³√2):12=1331√2:12 см³