Предмет: Алгебра,
автор: Аноним
Спасайте пожалуйста :) ВЫЧИСЛИТЬ
sin(П/4-a) , если sin a= корень из 2/3 и П/2 < a < П
Ответы
Автор ответа:
0
- корень из 2/ 2* на корень из 3 - 1/корень из 3
Приложения:
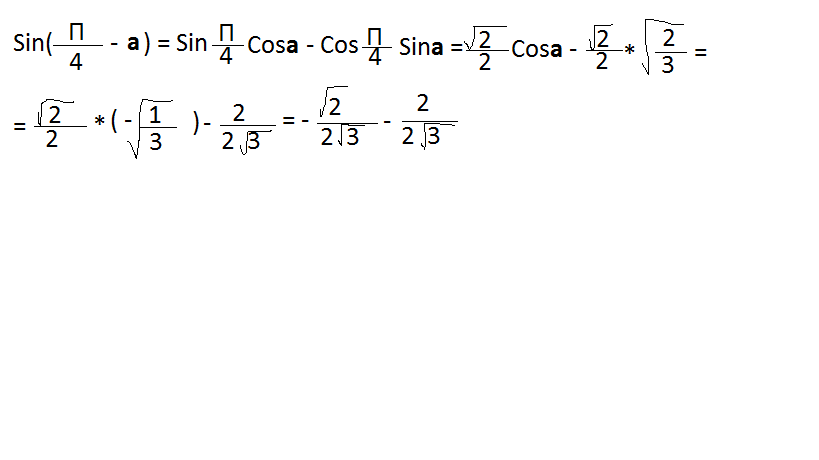
Автор ответа:
0
хорошо
Автор ответа:
0
картинка вверху,где ответ был
Автор ответа:
0
конечно спасибо, но жаль с ответом не сошлось(
Автор ответа:
0
извините тогда((
Автор ответа:
0
все равно спасибо)
Автор ответа:
0
Формула разности двух углов:
sin(π/4-α) = sin(π/4)*cos α - cos(π/4)*sin α =
=(√2/2)*cos α - (√2/2)*sin α = (√2/2)*(cos α - sin α).
сos α = √(1-sin²α)
Если sin a= корень из (2/3) и П/2 < a < П - это 2 четверть, косинус отрицателен. сos α = -√(1-2/3) = - 1 / √3.
Тогда sin(π/4-α) = (√2/2)*((- 1 / √3.)-√(2/3)).
sin(π/4-α) = sin(π/4)*cos α - cos(π/4)*sin α =
=(√2/2)*cos α - (√2/2)*sin α = (√2/2)*(cos α - sin α).
сos α = √(1-sin²α)
Если sin a= корень из (2/3) и П/2 < a < П - это 2 четверть, косинус отрицателен. сos α = -√(1-2/3) = - 1 / √3.
Тогда sin(π/4-α) = (√2/2)*((- 1 / √3.)-√(2/3)).
Приложения:
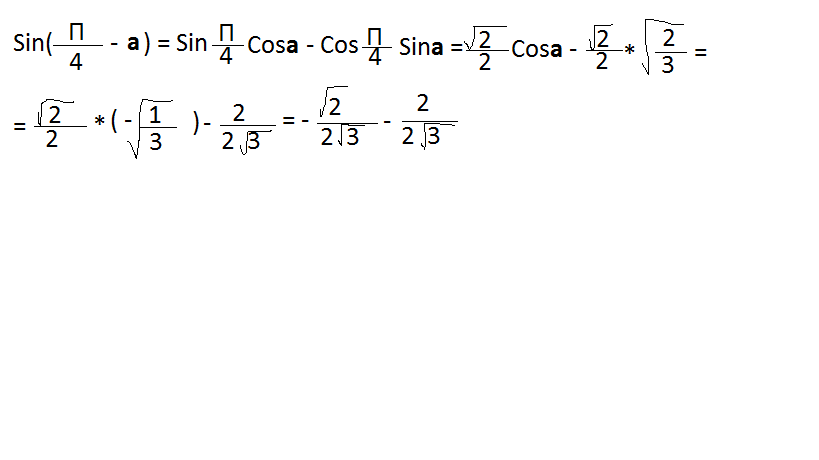
Автор ответа:
0
спасибо за решение, жаль ответ не сходится (
Похожие вопросы
Предмет: Биология,
автор: pavelshokin11
Предмет: Немецкий язык,
автор: nikev2015
Предмет: Математика,
автор: sidgiyayeva202085
Предмет: Химия,
автор: Didanacat