задание из гиа часть С в прямоугольном треугольнике АВС, катет АС=12,а катит ВС=5. Найдите радиус окружности которая проходит через концы гипотенузы треугольника и касается прямой ВС
Ответы
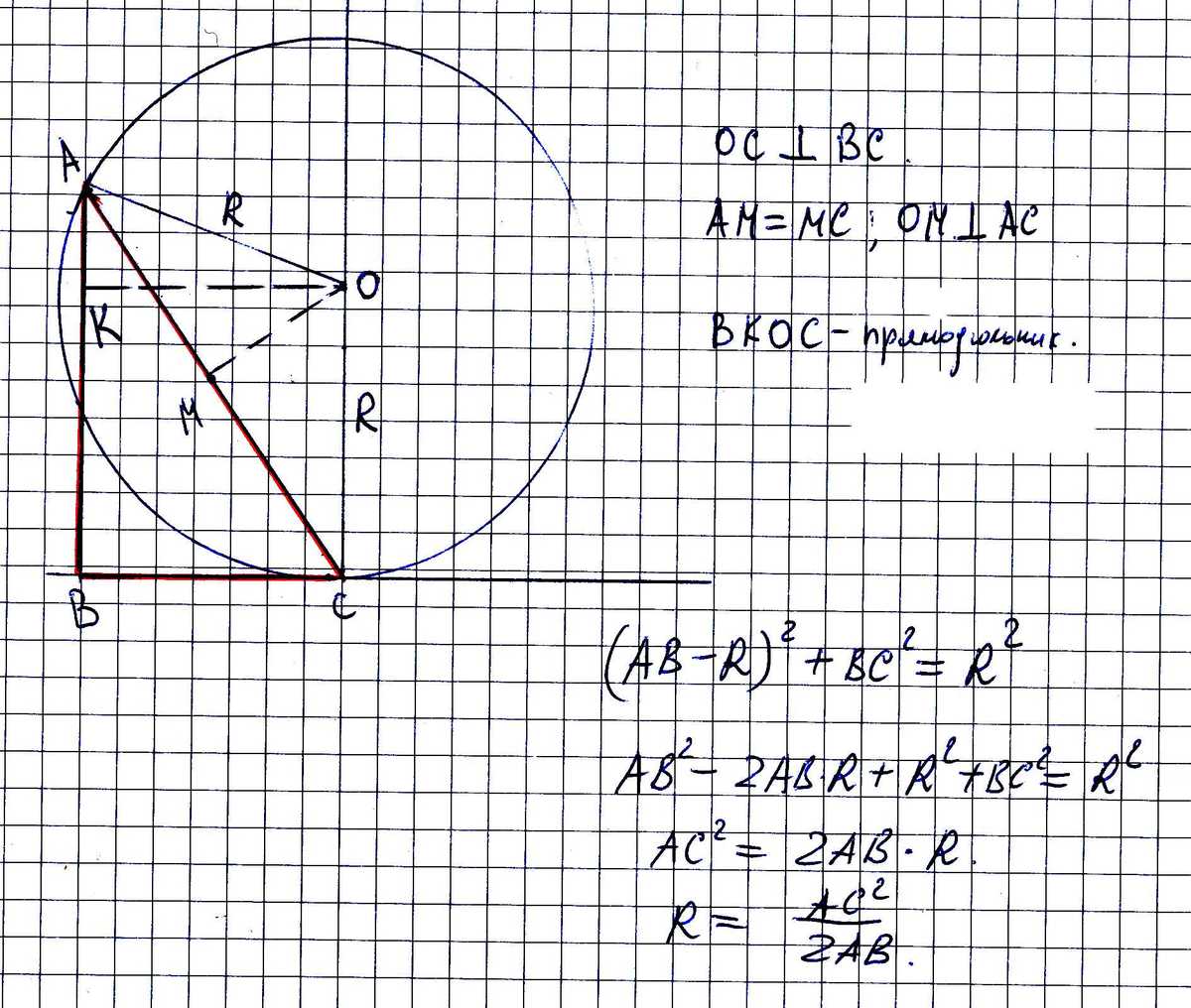
см чертеж. Пардон, я поменял точки В и С местами, уж простите.
У меня обозначено катет АВ = 12, а катет ВС=5. Гипотенуза обозначена АС. Ясно, что она равна 13 (это Пифагорова тройка 5;12;13), и окружность проходит через точки А и С.
Окружность проходит через точки А и С, и к тому же в точке С - касается (не может она в другой точке касаться, а в этой пересекать :))) так не бывает). То есть центр окружности лежит на пересечении перпендикуляра к ВС в точке С и перпендикуляра к АС в точке М - середине АС(то есть такая точка - единственная). Осталось найти на перпендикуляре из точки С к ВС такую точку О, что АО = ОС = R.
На рисунке приведено решение, суть его такова - проводим из О препендикуляр к АВ, получаем прямоугольник со сторонами R и ВС.
(АВ - R)^2 + BC^2 = R^2;
AC^2 = 2*AB*R; R = AC^2/(2*AB).
R = 13^2/24 = 169/24.