Question

помогите пожалуйста.

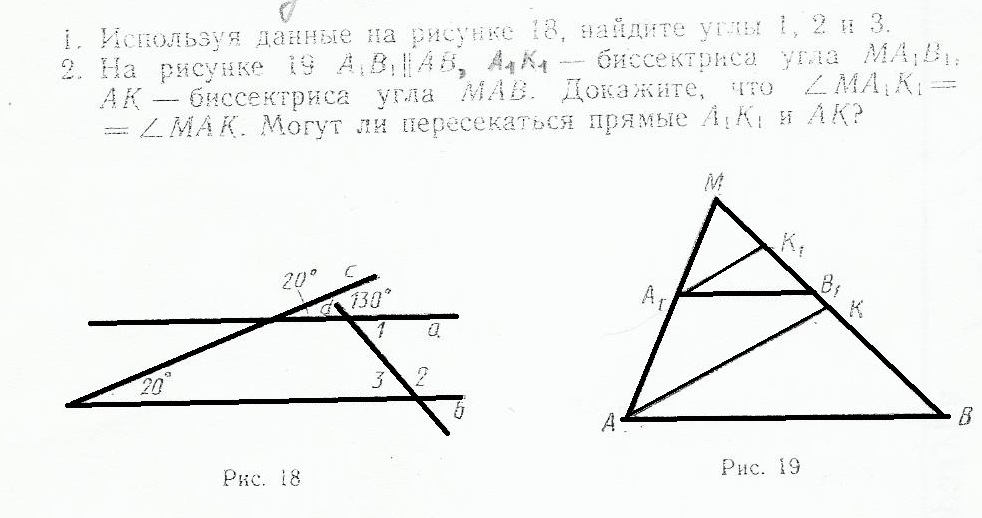
2)На рисунке 19 A1B1 ll AB, A1K1 ,биссектриса угла MA1B1 
AK- биссектриса угла MAB. Докажите, что угол MA1K1= углу MAK.
Могут ли пересекаться прямые А1К1 и АК

Answer 1

A1B1 ll AB, МА - секущая.
⇒
∠МА1В1=∠МАВ
A1K1 ,биссектриса угла MA1B1
AK- биссектриса угла MAB
Биссектрисы равных углов делят их на равные части.⇒
 угол MA1K1= углу MAK.
------
Прямые А1К1 и АК параллельны. т.к. соответственные углу АМ1КМ=МАК, поэтому они пересекаться не могут.