Предмет: Математика,
автор: terw63tew
Помогите вычислить предел. Расписать решение
Приложения:
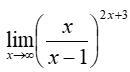
Ответы
Автор ответа:
1
Видимо, мало кто знает, что означает в степени +5 и что каждый предел будет равен единички, так как коэффициенты перед x единицы
Автор ответа:
0
Ответ:
Пошаговое объяснение:
Похожие вопросы
Предмет: Психология,
автор: olenabarchuk85
Предмет: Биология,
автор: kyzminovalena14
Предмет: География,
автор: lubomilkalukach
Предмет: Алгебра,
автор: Аноним
Предмет: Английский язык,
автор: ru59g5k4gz