Предмет: Алгебра,
автор: fedorchenkoa64
Вычислить интеграл. Пошагово.
Приложения:
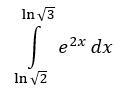
Ответы
Автор ответа:
1
Ответ: 0,5
Объяснение:
Вычислите интеграл
Вводим замену
Вычисляем определенный интеграл
#SPJ1
Похожие вопросы
Предмет: Другие предметы,
автор: Cohendd
Предмет: Алгебра,
автор: nurbakutaimeken
Предмет: Литература,
автор: dmakash1792
Предмет: История,
автор: Аноним