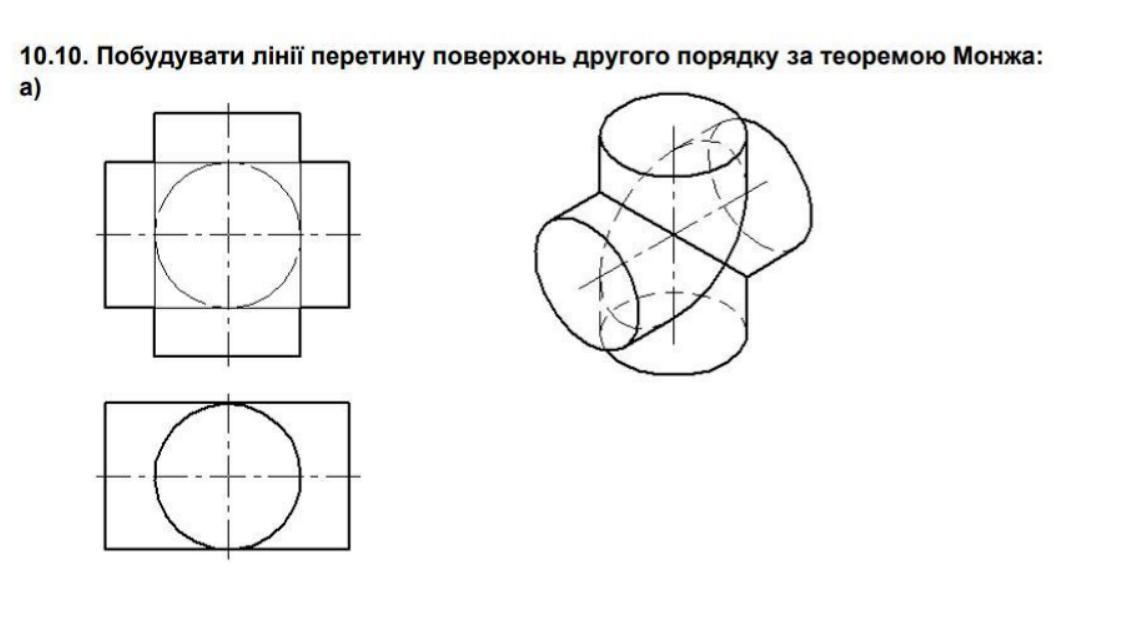
НАРЕСНА ГЕОМЕТРІЯ Побудувати лінії перетину поверхонь другого порядку за теоремою Монжа:
Ответы
Ответ:
Теорема Монжа (або теорема про лінії перетину поверхонь другого порядку) стверджує, що дві поверхні другого порядку взагалі можуть мати 4 точки перетину. Ця теорема допомагає побудувати ці точки перетину.
Для початку, нам потрібно мати рівняння двох поверхонь другого порядку. Такі рівняння мають загальний вигляд:
A₁x² + B₁y² + C₁z² + D₁xy + E₁xz + F₁yz + G₁x + H₁y + I₁z + J₁ = 0
A₂x² + B₂y² + C₂z² + D₂xy + E₂xz + F₂yz + G₂x + H₂y + I₂z + J₂ = 0
Де A₁, B₁, C₁, ..., J₁ та A₂, B₂, C₂, ..., J₂ - це коефіцієнти рівнянь.
Потім застосовуємо теорему Монжа, щоб знайти точки перетину. Це можна зробити шляхом розв'язання системи рівнянь для обох поверхонь. Це може бути складним завданням, оскільки розв'язання системи рівнянь вручну може бути дуже складним для поверхонь другого порядку.
Якщо ви хочете побачити візуальне представлення ліній перетину поверхонь другого порядку, ви можете скористатися програмами для візуалізації математичних об'єктів, такими як GeoGebra або MATLAB. Вони дозволяють побудувати графіки поверхонь та знаходити їх точки перетину.
Объяснение:
ось такі пироги