Question

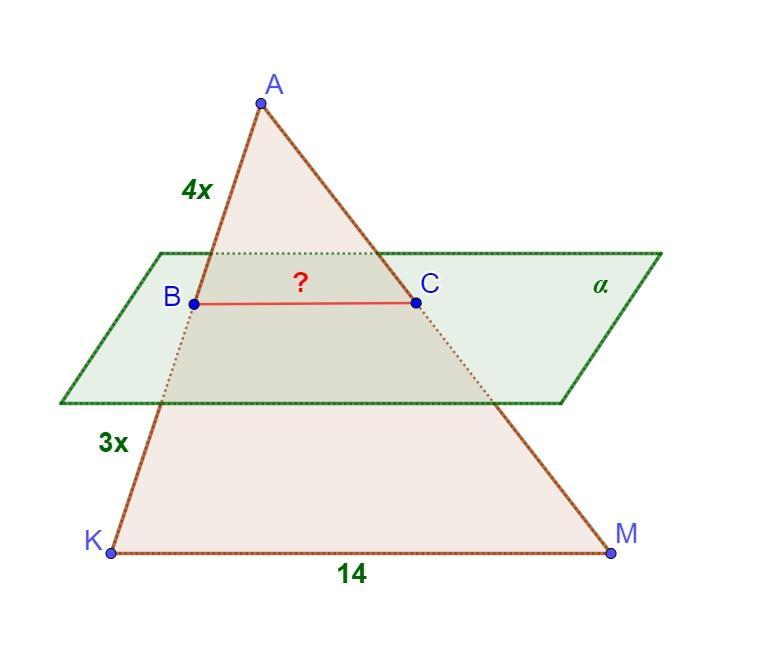
6. Дано трикутник АКМ. Площина а, паралельна прямій МК, перетинає сторону АК в точці В, а сторону АМ - в точці С. Знайти ВС, якщо МК=14 см, AB:BK=4:3.

Answer 1

Ответ:

ВC = 8 см

Объяснение:

Дано трикутник АКМ. Площина α, паралельна прямій МК, перетинає сторону АК в точці В, а сторону АМ - в точці С. Знайти ВС, якщо МК=14 см, AB:BK=4:3.

Розв'язання:

• Якщо площина проходить через пряму, паралельну іншій площині, і перетинає цю площину, то пряма їх перетину паралельна даній прямій.

Оскільки МК||α, і площина АКМ перетинає α по прямій ВС, то

МК||BC.

• Пряма, паралельна стороні трикутника, відтинає трикутник, подібний даному.

Отже, △АКМ ~ △АВС.

Тоді:

$\dfrac{AK}{AB} =\dfrac{KM}{BC}$

Позначимо АВ=4х, BK=3x, де х - коефіцієнт пропорційності.

Тоді АК=АВ+ВК=4х+3х=7х.

Отримаємо:

$\dfrac{7x}{4x}=\dfrac{14}{BC}$

$BC=\dfrac{4x\cdot 14}{7x}$

BC = 8

Таким чином, ВC = 8 см.

#SPJ1