Question

Діаметр кулі поділений двома точками на 3 частини, у відношенні 2:3:5. Знайти відношення площ перерізів кулі, які проходять через ці точки перпендикулярно діаметру.

Answer 1

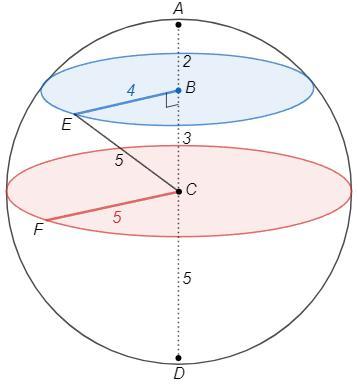
На диаметре шара AD взяты точки B и C.

AB:BC:CD =2:3:5

Понятно, что C - середина AD, т.е. центр шара.

Любое сечение шара - круг.

Пусть радиус шара CD=5, тогда BC=3

Круг с центром C имеет радиус шара, CF=5

Круг с центром B имеет радиус BE. Найдем его.

Сечение перпендикулярно диаметру - радиус в плоскости сечения перпендикулярен диаметру, BE⊥AD.

CE=5 (радиус шара)

BE =√(CE^2-BC^2) =4 (т Пифагора)

S_b/S_c =п BE^2 /п CF^2 =16/25