(1+x^3)dy=3x^2ydx
Помогите пожалуйста
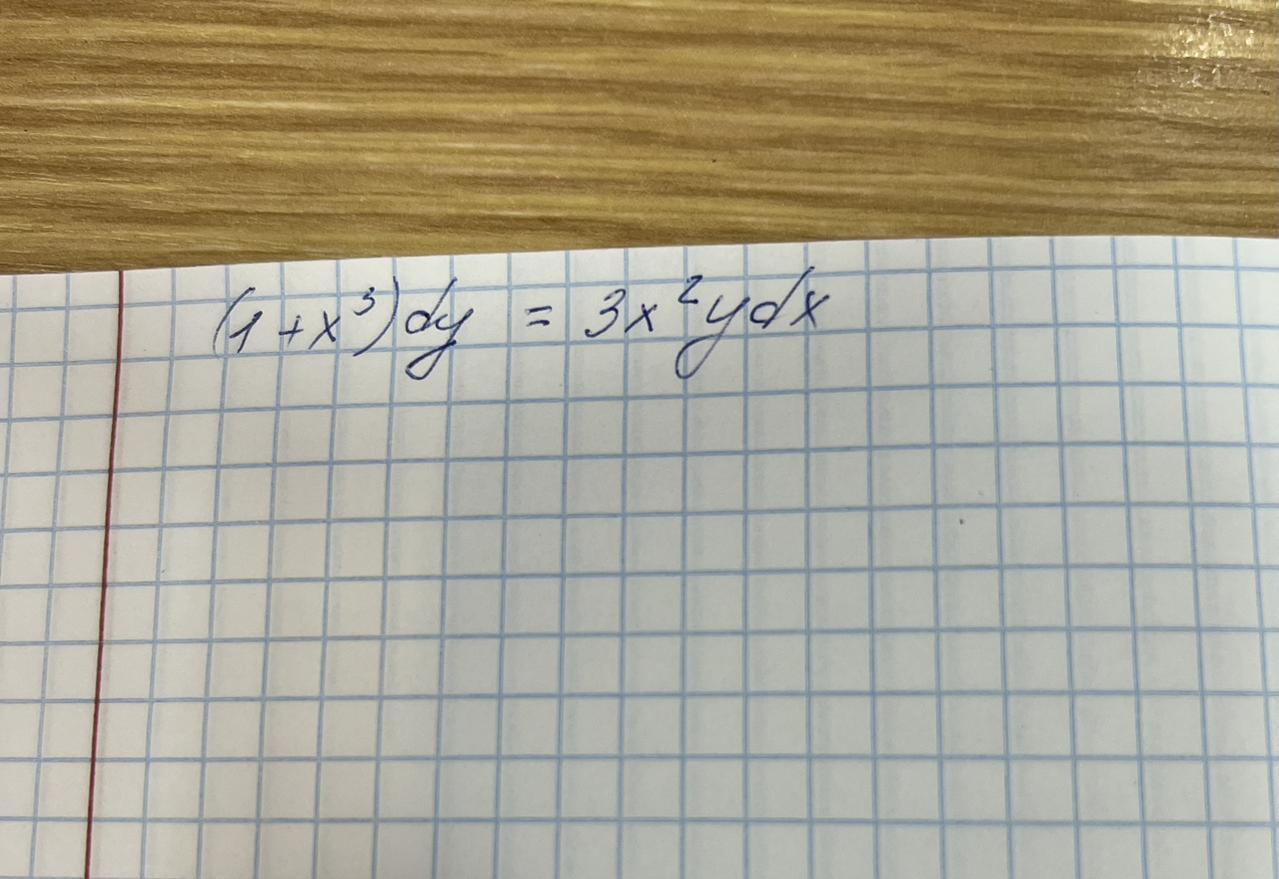
Ответы
Ответ:
Чтобы решить это дифференциальное уравнение, мы можем переставить его так, чтобы разделить переменные dy и dx.
Начиная с: (1+x^3)dy = 3x^2ydx
Разделим обе части на (1+x^3):
dy/dx = (3x^2y)/(1+x^3)
Теперь мы можем разделить переменные, умножив обе части на dx и разделив на y(1+x^3):
(1/(y(1+x^3)))dy = (3x^2)dx
Интеграция обеих сторон:
∫(1/(y(1+x^3)))dy = ∫(3x^2)dx
Для вычисления интегралов можно использовать замену u = 1+x^3, du = 3x^2dx:
∫(1/(y(1+x^3)))dy = ∫du/y
Что упрощает:
ln|у| = ln|u| + С
Где C — константа интегрирования. Теперь подставим обратно u = 1+x^3:
ln|у| = ln|1+x^3| + С
Наконец, мы можем возвести в степень обе части, чтобы исключить логарифмы:
|у| = |1+x^3|e^C
Поскольку C — произвольная константа, заменим ее на C1 (еще одну произвольную константу):
|у| = |1+x^3|e^C1
Абсолютные значения можно удалить, поскольку любая константа может быть положительной или отрицательной, поэтому мы можем написать:
у = (1+х^3)е^C1
Мы можем еще больше упростить, заменив e^C1 другой константой, назовем ее C2:
у = (1+х^3)C2
Итак, общее решение дифференциального уравнения дается уравнением y = (1+x^3)C2, где C2 — произвольная константа.
Пошаговое объяснение:
так нужно