Предмет: Математика,
автор: Sonalik
(1+x^3)dy=3x^2ydx
Помогите пожалуйста
Приложения:
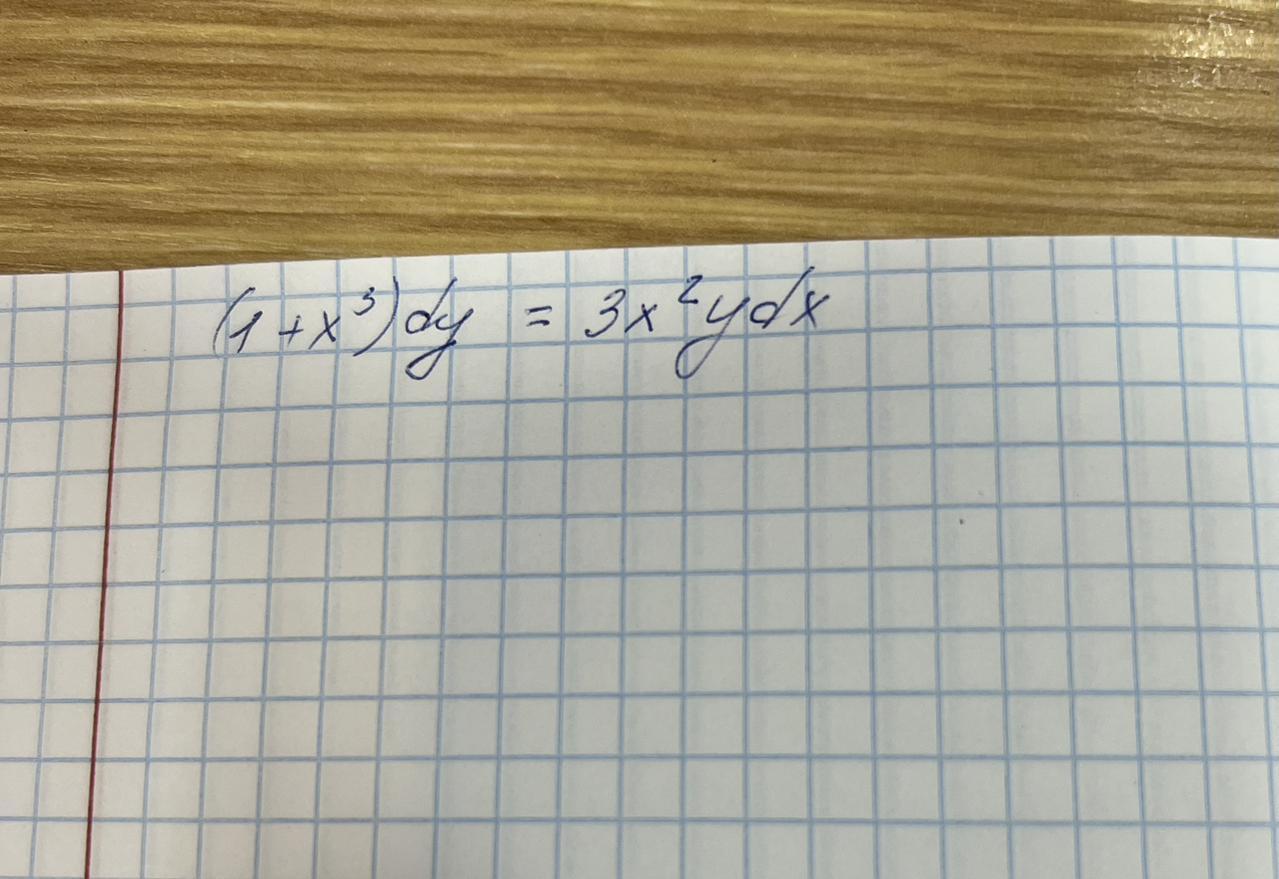
Ответы
Автор ответа:
0
Пошаговое объяснение:
1+x^3)dy=3x^2ydx.
Для начала, разделим обе части на (1+x^3):
(dy)/(y)=(3x^2dx)/(1+x^3).
Теперь проинтегрируем обе части уравнения:
∫(dy)/(y)=∫(3x^2dx)/(1+x^3).
Левая часть дает ln|y|, а правая часть требует небольшой замены переменной: x^3 = u, тогда dx = (1/3u^(-2/3))du.
Используя это, мы получим:
ln|y| = ∫(3x^2dx)/(1+x^3) = ∫(3/u)/(1+u)du.
Продолжаем решать:
ln|y| = 3∫(du)/(u(1+u)).
Разделим на 3 и разложим дробь на простые дроби:
(1/u-1/(1+u))du.
Теперь интегрируем:
ln|y| = 3(ln|u|-ln|1+u|)+C.
Подставляем обратные замены для u и y:
ln|y| = 3(ln|x^3|-ln|1+x^3|)+C.
Итак, решение дифференциального уравнения будет:
ln|y| = 3ln|x^3/(1+x^3)|+C.
Похожие вопросы
Предмет: Другие предметы,
автор: stanislavabogoslova
Предмет: Физика,
автор: anmsbd
Предмет: Математика,
автор: kruzor31
Предмет: Математика,
автор: syzdykovaalfia95
Предмет: Алгебра,
автор: mandarin0104