Question

Знайти площу ...... криволінійної фігури, обмеженої кривою ...... та прямою ........ .

Answer 1

Ответ:

$\displaystyle S=\frac{32}{3}$

Объяснение:

Формула для расчета площади криволинейной трапеции

$\displaystyle S=\int\limits^a_b {\bigg(y_1(x) -y_2(x)\bigg)} \, dx$

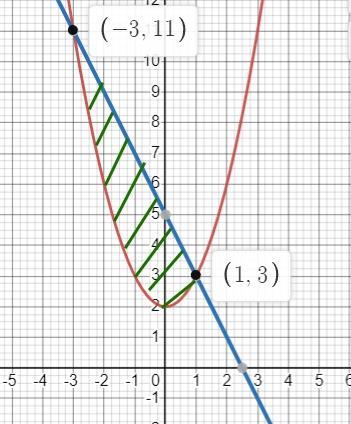
Делаем чертежи функций и определяем всё, что нужно для интегрирования.

b = -3

a = 1

y₁(x) = 5 - 2x     (2x+y=5) - график лежит "выше"

y₂(x) = x² + 2

Считаем площадь

$S=\int\limits^1_{-3} {\bigg(5-2x-x^2-2\bigg)} \, dx =\\\\\\=\int\limits^1_{-3} {-x^2} \, dx -2\int\limits^1_{-3} {x} \, dx +3\int\limits^1_{-3} {} \, dx =\bigg(\displaystyle -\frac{x^3}{3} -2\frac{x^2}{2} +3x\bigg)\bigg|_{-3}^1=-\frac{28}{3} +8+12=\frac{32}{3}$