Question

найдите площадь трапеции АВСД с основанием АД и ВС, если АВ=12см, ВС=14см, АД=30см, <В=150 градусов помогите решить
 

Answer 1

Площадь трапеции равна произведению полусуммы оснований на высоту.На чертеже трапеции опустите высоту из угла В на основание АД - получите прямоугольный треугольник с углом при точке В, образованным стороной АВ и высотой, в 60 градусов и противолежащим высоте углом в 30 градусов.Высота определится из этого полученного прямоугольного треугольника, как катет прямоугольного треугольника, лежащий против угла в 30 градусов, который равен половине гипотенузы, то есть стороны АВ:h = AB/2 = 6 (см).Площадь:S = h(АД + ВД)/2 = 132 (см2).

Answer 2

спасибо

Answer 3

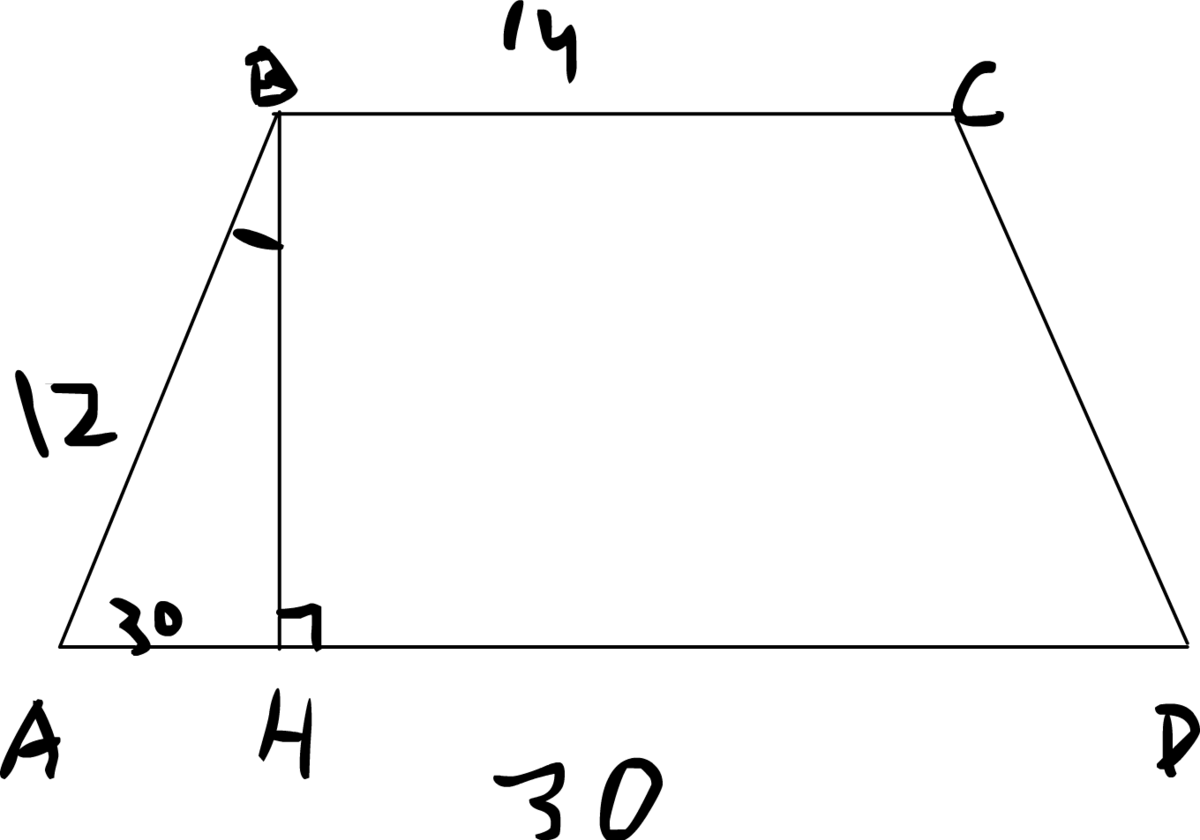
Я Изобразил конструкцию задачи на прикрепленном рисунке.
Дополнительное построение: опустим из вершины В на АД высоту ВН.
угол АВС = 150, угол НВС = 90, т.к. это высота. тогда угол АВН=150-90=60.
В треугольнике АВН угол Н = 90, В = 60, тогда угол А=30.
По теореме прямоугольного треугольника, катет, напротив угла в 30 градусов, в 2 раза меньше гипотенузы. Гипотенуза АВ=12, => ВН=6 см.
Площадь трапеции равна 1/2 (ВС+АD)ВH = 1/2 (14+30)6 = 1/2 * 264 = 132 см^2.
Ответ: 132 см^2.

Answer 4

спасибо