Предмет: Алгебра,
автор: fctdgsygfdhngfxzgsac
Обчислити інтеграл заміною змінних.
Приложения:

Ответы
Автор ответа:
1
Ответ:
Вычислить определённый интеграл .
Применяем метод замены переменной в определённом интеграле .
Приложения:
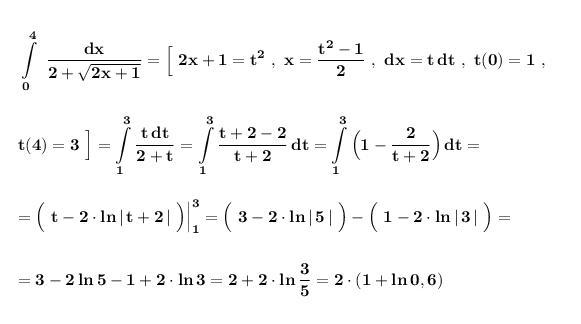
fctdgsygfdhngfxzgsac:
спасибо большое)
Похожие вопросы
Предмет: Физика,
автор: sonchs2023
Предмет: Геометрия,
автор: pud8ras
Предмет: Французский язык,
автор: mishamisha10092011
Предмет: Алгебра,
автор: kb735755
Предмет: Английский язык,
автор: Аноним