Question

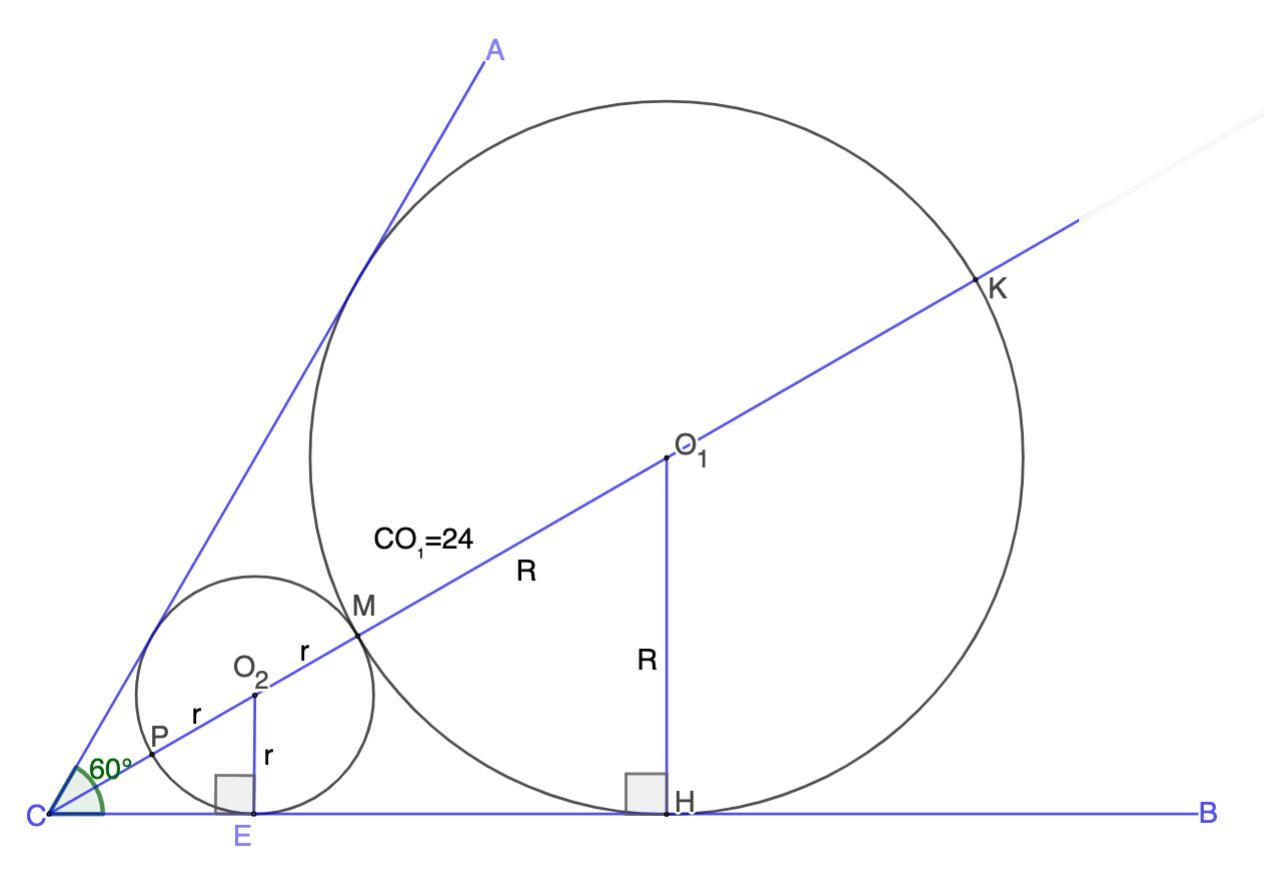
В5. Две окружности с центрами в точках О, и О, касаются друг друга
и сторон угла АСВ, равного 60°. Известно, что расстояние от верши-
ны угла до центра О, большей окружности равно 24. Найдите рас-
стояние от вершины угла до центра О, меньшей окружности.

Answer 1

Ответ:

Расстояние от вершины угла до центра О₂ меньшей окружности равно 8 ед.

Объяснение:

В5. Две окружности с центрами в точках О₁ и О₂ касаются друг друга и сторон угла АСВ, равного 60°. Известно, что расстояние от вершины угла до центра О₁ большей окружности равно 24. Найдите расстояние от вершины угла до центра О₂ меньшей окружности.

Дано: ∠АСВ = 60°.

Окр.(О₁,R) и Окр.(О₂,r) - вписанные;

Окр.(О₁,R) и Окр.(О₂,r) касаются друг друга в точке М;

СО₁ = 24.

Найти: СО₂

Решение:

• Центр вписанной окружности лежит на биссектрисе угла.

⇒   ∠АСК = ∠КСВ = 30°

Рассмотрим ΔСО₁Н.

• Радиус, проведенный в точку касания перпендикулярен касательной.

⇒ ∠СО₁Н = 90°

• Катет, лежащий против угла в 30°, равен половине гипотенузы.

⇒   О₁Н = R = 24 : 2 = 12.

Рассмотрим ΔСО₂Е - прямоугольный.

∠О₂СЕ = 30°   ⇒   СО₂ = 2О₂Е = 2r

CO₁ = CO₂ + O₂M + MO₁

24 = 2r + r + 12

3r = 12   |:3

r = 4

CO₂ = 2r = 8

Расстояние от вершины угла до центра О₂ меньшей окружности равно 8 ед.

#SPJ1