Предмет: Алгебра,
автор: ssolomon77777
помогите решить методом замены
Приложения:
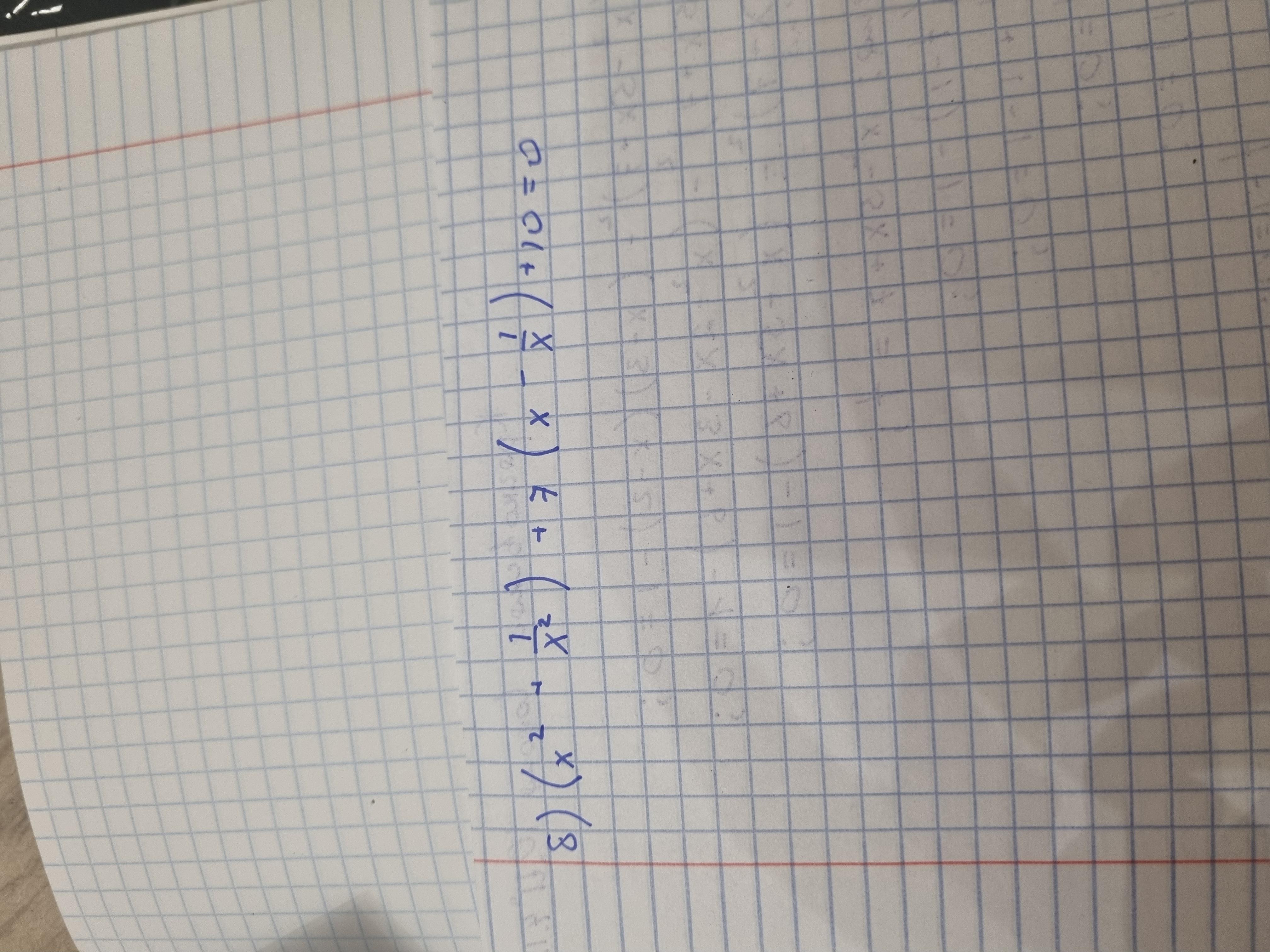
Ответы
Автор ответа:
0
Похожие вопросы
Предмет: Литература,
автор: lalilu12
Предмет: Геометрия,
автор: sssbliattim64
Предмет: Українська література,
автор: evakorolevason
Предмет: Қазақ тiлi,
автор: Аноним