Предмет: Алгебра,
автор: nikolostv50002
Розв'язати нерівність |х - 5|(x + 3) > 0.
Ответы
Автор ответа:
2
Ответ:
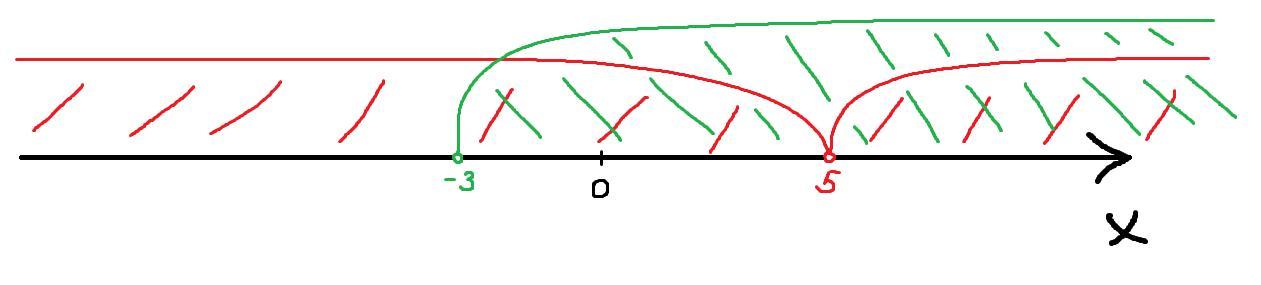
(-3; 5) ∪ (5; +∞)
Объяснение:
|x - 5|(x + 3) > 0
|x - 5| не може дорівнювати нулю, тому що вираз має бути більше 0. При всіх інших значеннях буде значення модуля більше 0.
x - 5 ≠ 0
x ≠ 5
x + 3 > 0
x > -3
Корені нерівності знаходяться на проміжку (-3; 5) ∪ (5; +∞)
Автор ответа:
0
Ответ:
Объяснение:
Нет ответа (значение
под модулем не может быть
меньше нуля!)
Приложения:
Похожие вопросы
Предмет: Алгебра,
автор: andrejbebrik22
Предмет: Экономика,
автор: anastasiadob77
Предмет: Другие предметы,
автор: evgenijtolstaj452
Предмет: Математика,
автор: russudianna08
Предмет: Немецкий язык,
автор: Аноним