визначте чи рівносильні рівняня
a) 3x+5=8 i x-1/x²-1 =0
б)2x+3=9 i x-3/x-5=0
в)2x=10 i x+5/x-5 =0
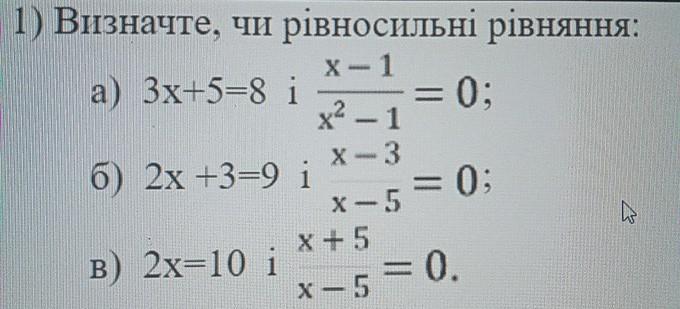
Ответы
Ответ и Объяснение:
Требуется определить равносильные ли уравнения.
Информация. Два уравнения называют равносильными, если они имеют одинаковые корни или если оба уравнения не имеют корней.
Решение. Решим каждую пару уравнений и сравним корни.
а) 3·x+5 = 8 ⇔ 3·x = 8-5 ⇔ 3·x = 3 ⇔ x = 1
→ определим множество допустимых значений:
x²-1 ≠0 ⇒ x ≠ ±1.
Значит, x = 1 не является корнем уравнения, то есть уравнения не равносильны.
б) 2·x+3 = 9 ⇔ 2·x = 9-3 ⇔ 2·x = 6 ⇔ x = 3
→ определим множество допустимых значений:
x-5 ≠0 ⇒ x ≠ 5.
Тогда
Значит, x = 3 является корнем обоих уравнений и поэтому уравнения равносильны.
в) 2·x = 10 ⇔ x = 5
→ определим множество допустимых значений:
x-5 ≠0 ⇒ x ≠ 5.
Значит, x = 5 не является корнем уравнения, то есть уравнения не равносильны.
#SPJ1