Question

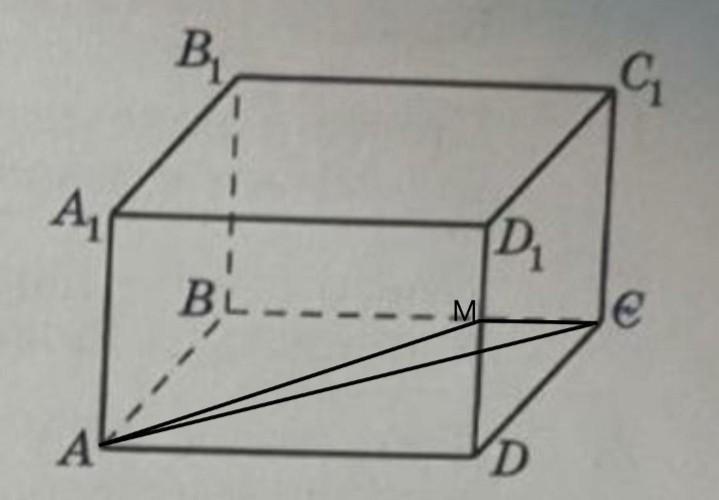
ABCDA1B1C1D1 — прямокутний паралелепіпед, AB=5 см, AD=12 см , AA1 = 24 см Побудувати переріз паралелепіпеда площиною, яка проходить через точки А, C i K - середину ребра DD1 Знайти периметр отриманого перерізу.​

Answer 1

Ответ:

S(∆ACM)=6√194см²

МD=DD1/2=24/2=12см

∆АМD- прямокутний трикутник

Теорема Піфагора:

АМ=√(АD²+MD²)=√(12²+12²)=

=12√2см

∆МСD- прямокутний трикутник.

Теорема Піфагора:

МС=√(DC²+MD²)=√(5²+12²)=13см.

∆АСD- прямокутний трикутник

Теорема Піфагора:

АС=√(АD²+DC²)=√(12²+5²)=13см.

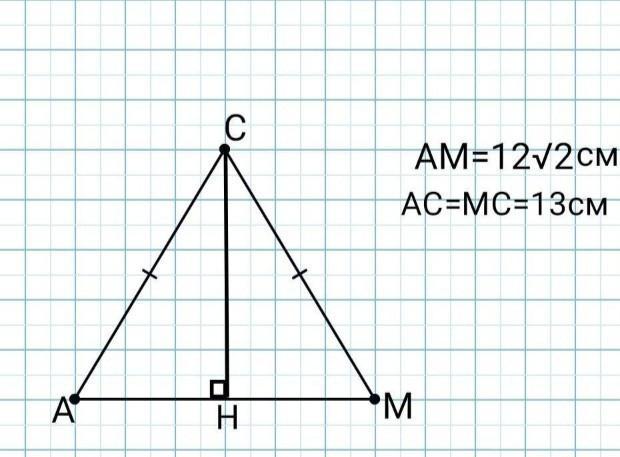
AH=HM

AH=AM/2=12√2/2=6√2см

∆АСН- прямокутний трикутник.

Теорема Піфагора:

СН=√(АС²-АН²)=√(13²-(6√2)²)=

=√(169-72)=√97см.

S(∆ACM)=½*AM*CH=½*12√2*√97=

=6√1 S(∆ACM)=6√194см² МD=DD1/2=24/2=12см ∆АМD- прямокутний трикутник Теорема Піфагора: АМ=√(АD²+MD²)=√(12²+12²)= - 2

Ответ: S(∆ACM)=6√194см² Объяснение: МD=DD1/2=24/2=12см ∆АМD- прямокутний трикутник Теорема Піфагора: АМ=√(АD²+MD²)=√(12²+12²)= - 1