Предмет: Алгебра,
автор: fctdgsygfdhngfxzgsac
Користуючись методом розкладу, обчислити інтеграли.
Приложения:
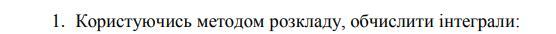
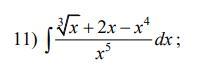
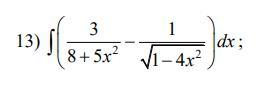
Ответы
Автор ответа:
1
Ответ:
Найти неопределённый интеграл .
Приложения:
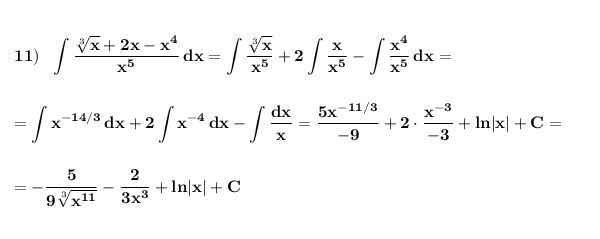
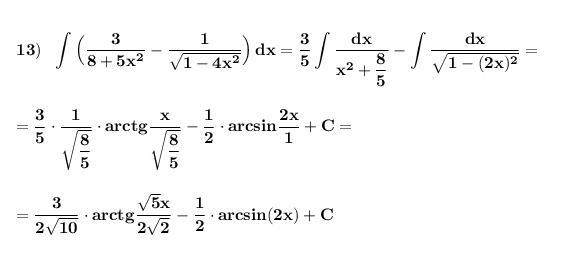

fctdgsygfdhngfxzgsac:
спасибо большое)
Похожие вопросы
Предмет: Литература,
автор: sofiasylka9
Предмет: География,
автор: ksenwianrik
Предмет: История,
автор: ZhanerkeboZhanerkebo
Предмет: Математика,
автор: rustem09121975
Предмет: Қазақ тiлi,
автор: daripbaeva