Предмет: Алгебра,
автор: bajuzahakarys
срочно дам 50 баллов
Приложения:
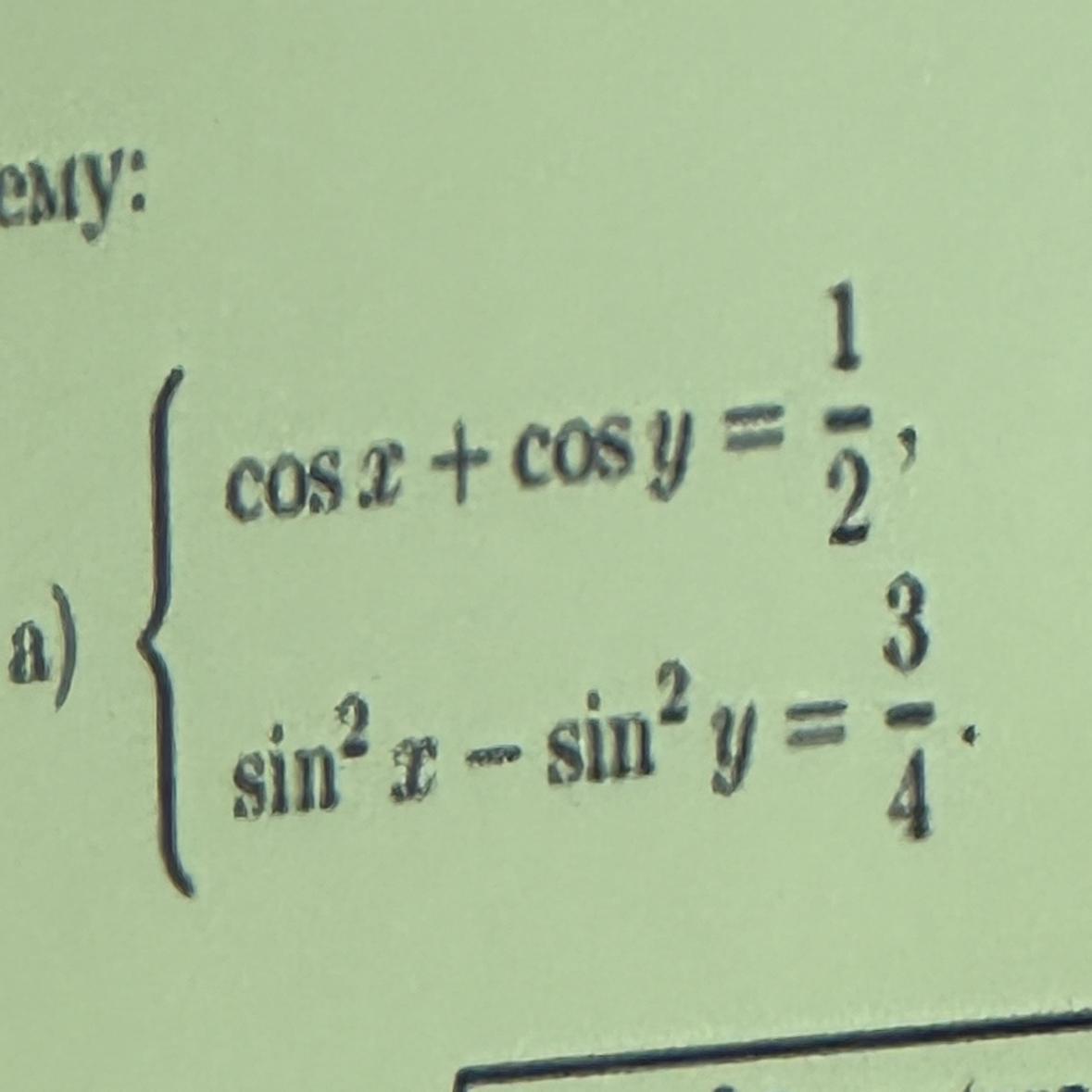
Ответы
Автор ответа:
0
Ответ:
Складываем:
сosx·cosy+sinx·siny=a²+1⇒cos(x-y)=a²+1
Вычитаем:
сosx·cosy-sinx·siny=a²-1⇒cos(x+y)=a²-1
Получаем систему двух уравнений:
{cos(x-y)=a²+1
{cos(x+y)=a²-1
Первое уравнение имеет решения при
-1≤a²+1≤1⇒a=0
Второе уравнение имеет решения при
-1≤a²-1≤1⇒0≤a²≤2
Общим значением а, удовлетворяющим и первому и второму уравнению является a=0
{cos(x-y)=1⇒x-y=2πk, k∈Z
{cosx(x+y)=-1⇒x+y=π+2πn, n∈Z
2x=π+2πm, m∈Z ( m=k+n)
x=(π/2)+πm, m∈Z
y=(π/2)+πp, p∈Z
О т в е т. при а=0
x=(π/2)+πm, m∈Z
y=(π/2)+πp, p∈Z
Похожие вопросы
Предмет: Геометрия,
автор: babenko198530
Предмет: Геометрия,
автор: ggprotop01
Предмет: Биология,
автор: jdkdjjs
Предмет: Физика,
автор: rmuzaparova
Предмет: Математика,
автор: Аноним