Question

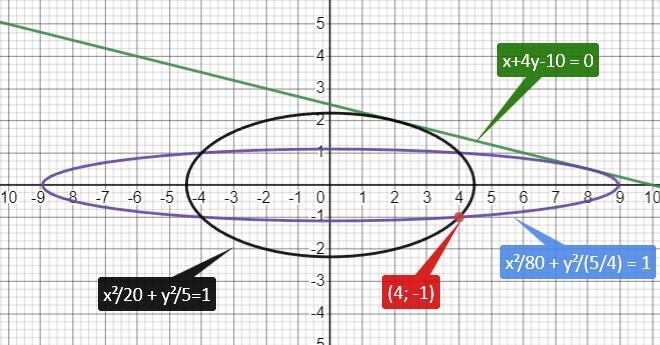
скласти рівняння еліпса, який проходить через точку А(4;-1) і дотикається до прямої x+4y-10=0, якщо його осі збігаються з координатними осями

Answer 1

Ответ:

$\displaystyle \boldsymbol{\frac{x^2}{20}+\frac{y^2}{5}=1 }\\\\\\\displaystyle \boldsymbol{\frac{x^2}{80}+\frac{y^2}{5/4}=1 }$

Объяснение:

Условие касания прямой y = mx + k и эллипса  $\displaystyle \frac{x^2}{a^2} +\frac{y^2}{b^2} =1$  

выражается формулой k² = m²a² + b²

Приведем нашу прямую  к виду y = mx + k

x + 4y - 10=0

4у = 10 - х

$\displaystyle y=-\frac{1}{4} x+\frac{5}{2}$

тогда у нас

k = 5/2

m = -1/4

Теперь в условие подставим эти значения

$\displaystyle \bigg(\frac{5}{2} \bigg)^2=\bigg(-\frac{1}{4} \bigg)^2a^2+b^2\\\\\\\frac{25}{4} =\frac{1}{16} a^2+b^2$

это будет первым уравнение системы.

вторым уравнением будет собственно уравнение эллипса, проходящего через точку А(4; -1)

$\displaystyle \frac{4^2}{a^2} +\frac{(-1)^2}{b^2} =1$

Мы получили систему двух уравнений с двумя неизвестными а и b

$\displaystyle \left \{ {{\displaystyle \frac{25}{4}=\frac{1}{16}a^2+b^2 } \atop {\displaystyle \frac{16^2}{a^2}+\frac{1}{b^2} =1}} \right.$

Теперь осталось только решить систему.

Умножаем первое уравнение на 16, второе на a²b²

$\displaystyle \left \{ {{a^2+16b^2-100=0} \atop {16b^2+a^2-a^2b^2=0}} \right.$

Из системы получаем a²b² = 100

Обозначим а² = x;  b² = y.

запишем

$\displaystyle xy=100\quad \Rightarrow \quad x=\frac{100}{y}$

подставим это в уравнение 16b² + a² -a²b² =0

или

16у + х -ху =0

$\displaystyle 16y +\frac{100}{y} -100=0\\\\\\16y^2-100y+100=0\\\\\\D=(-100)^2-4*16*100=3600\\\\\sqrt{D} =60\\\\y_1=\frac{-b-\sqrt{D} }{2a} =\frac{100-60}{32} =\frac{5}{4} \\\\\\y_2=\frac{-b+\sqrt{D} }{2a} =\frac{100+60}{32} =5$

Тогда х₁ = 80;  х₂ = 20

Т.е. мы имеем пары х₁ = 80;  y₁ = 5/4    и  x₂=20;  y₂=5

Теперь вспомним, что а² = x;  b² = y

и напишем уравнения двух эллипсов

$\displaystyle \boldsymbol{\frac{x^2}{20}+\frac{y^2}{5}=1 }\\\\\\\displaystyle \boldsymbol{\frac{x^2}{80}+\frac{y^2}{5/4}=1 }$

чертеж прилагается