Предмет: Алгебра,
автор: Аноним
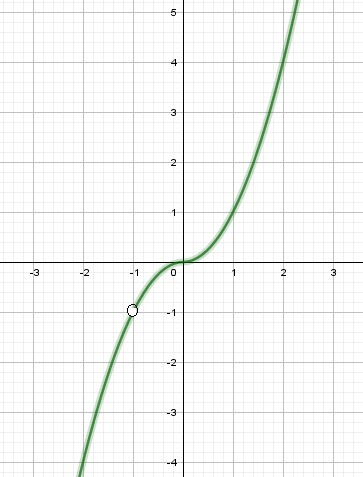
Постройте график функции y=(x^2+x)|x|/x+1 и определите, при каких значениях с прямая y=с не имеет с графиком ни одной общей точки/ 
Ответы
Автор ответа:
0
Область определения: функция существует, если знаменатель дроби не обращается в нуль.
Упростим исходную функцию
y = c - прямая, параллельная оси Ох.
При с = - 1 графики не имеют общих точек
Приложения:
Похожие вопросы
Предмет: Окружающий мир,
автор: frenchrxses
Предмет: Геометрия,
автор: reginakarpova210
Предмет: Алгебра,
автор: fregcxx
Предмет: Алгебра,
автор: Дамдин150