Question

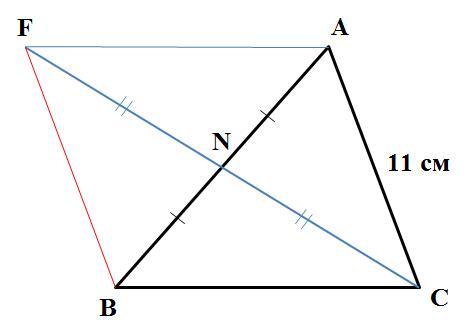
- На продовженні медіани CN трикутника АВС за точку N відклали відрізок NF, рівний відрізку CN. Знайдіт довжину відрізка FB, якщо АС = 11 см.​

Answer 1

Ответ:

Длина отрезка FB = 11 см

Объяснение:

Перевод: На продолжении медианы CN треугольника АВС за точку N отложили отрезок NF, равный отрезку CN. Найдет длину отрезка FB, если АС = 11 см.

Информация. 1) Признак параллелограмма:

• диагонали пересекаются и точкой пересечения делятся пополам.

2) Свойство параллелограмма:

• противоположные стороны параллелограмма параллельны и равны.

Решение. По условию:

1) CN медиана и по определению медианы делит сторону AB пополам: AN = NB;

2) NF = CN и поэтому отрезок CF делится точкой N.

Рассмотрим четырёхугольник ACBF (см. рисунок), Учитывая 1) и 2) по признаку параллелограмма получаем, что четырёхугольник ACBF - параллелограмм.

Далее, по свойству параллелограмма противоположные стороны параллелограмма ACBF параллельны и равны:

AC || BF, AF || CB, AC = BF, AF = CB.

Так как АС = 11 см, то BF = АС = 11 см.

#SPJ1