Предмет: Геометрия,
автор: solokha2603
Дві сторони трикутника дорівнюють 8 см і 10 смі утворюють кут 60 градусів. Знайдіть радіус кола, описаного
Ответы
Автор ответа:
0
Дано:
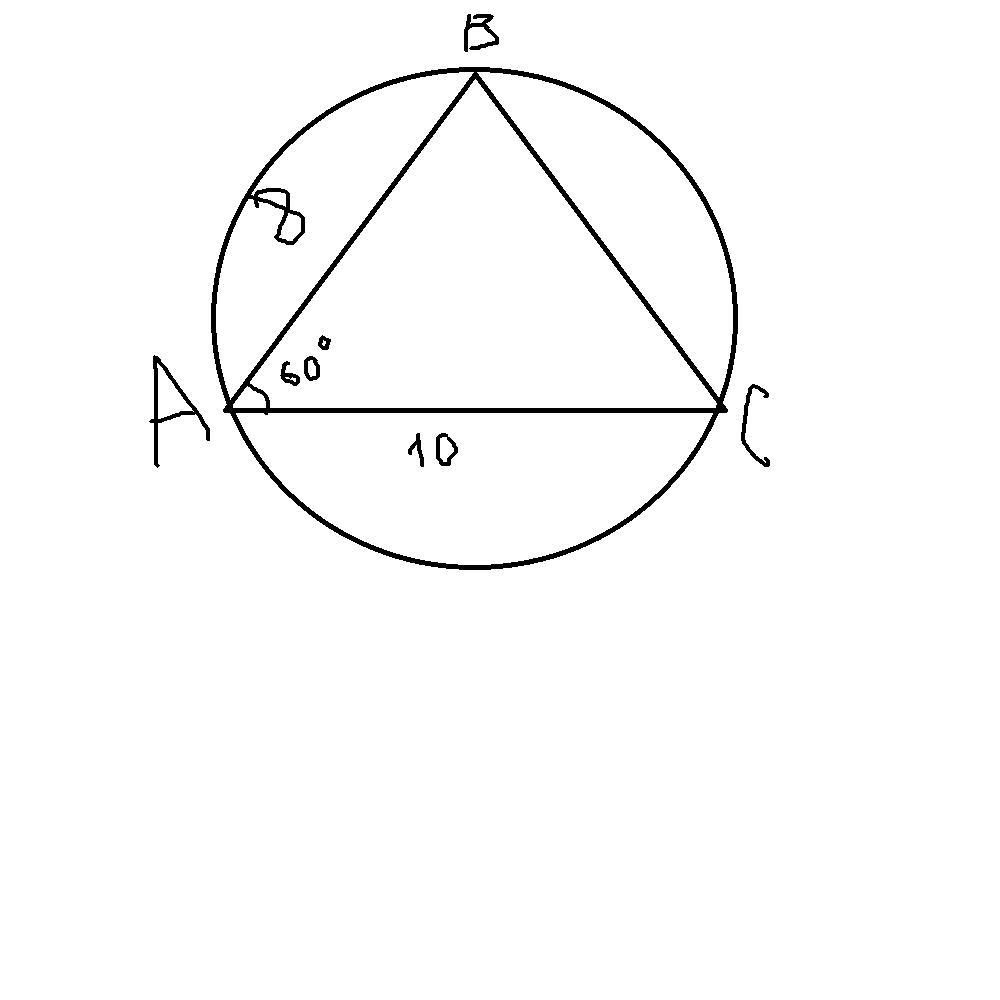
Δ ABC,
AB = 8, AC = 10
∠BAC = 60°
Найти:
R - ?
Решение:
1) Найдём сторону BC, по теореме косинусов.
≈ 9.
2) Найдём полупериметр.
3) Найдём площадь треугольника по теореме Герона.
≈ 34
4) Найдём радиус описанной окружность.
≈ 5.2
Ответ: R ≈ 5.2
Приложения:
Похожие вопросы
Предмет: Другие предметы,
автор: gremm201636
Предмет: Физика,
автор: ismartsdn01032022
Предмет: Русский язык,
автор: kasimoverzhan77
Предмет: Русский язык,
автор: daanaramazan085
Предмет: Биология,
автор: polinapolina234567