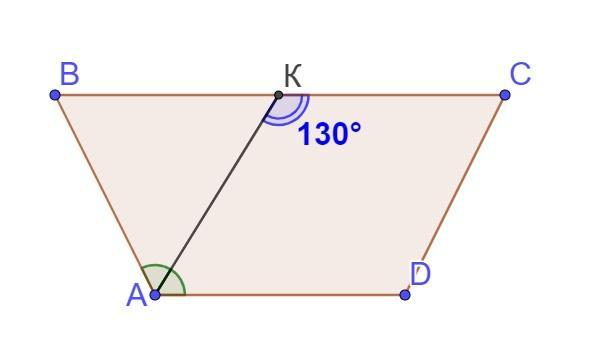
ABCD - рівнобічна трапеція AB=CD. АК бісектриса, перетинає сторону ВС в точці К.
Кут АКС=130º знайти кути трапеції.
Ответы
Ответ:
Кути трапеції дорівнюють 100°, 80°, 100°, 80°.
Объяснение:
ABCD - рівнобічна трапеція AB=CD. АК бісектриса, перетинає сторону ВС в точці К. Кут АКС=130º. знайти кути трапеції.
Нехай ABCD - дана рівнобічна трапеція, BC║AD, AB=CD, АК-бісектриса, АК∩ВС=К, ∠АКС=130°.
Знайдемо кути трапеції.
1) ∠АКС і ∠АКВ - суміжні, їх сума дорівнює 180°.
∠АКС + ∠АКВ = 180°
∠АКВ = 180° - ∠АКС = 180° - 130° = 50°
2) ∠КАD = ∠АКВ = 50° - як внутрішні різносторонні при BC║AD і січній АК.
3) ∠А = 2 · ∠КАD = 2 · 50° = 100° (АК-бісектриса ∠А)
4) ∠D=∠A=100° - як кути при основі рівнобічної трапеції.
5) ∠А+∠В=180° - як кути, прилеглі до бічної сторони трапеції.
∠В = 180° - ∠А = 180° - 100° = 80°
6) ∠С = ∠В = 80° - як кути при основі рівнобічної трапеції.
Відповідь: ∠А=∠D=100°, ∠В=∠С=80°
#SPJ1