Question

417. На числовом луче взяли два отрезка. координаты концов первого отрезка Депин на 6 равных частей, второй 18 и 22. координаты второго 19 и 20. Первый отрезок раз- шите обыкновенные дроби. соответствующие - на 10 равных частей. Напи- серединам каждого отрезка. п сравните их.​

Answer 1

Ответ:

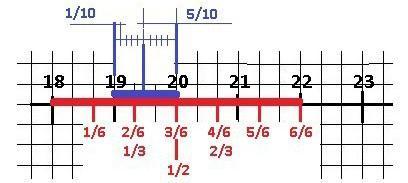
Рисунок к задаче в приложении.

РЕШЕНИЕ.

В задаче надо делить на 6 частей и, поэтому, за единицу лучше взять 3 клетки.

1) Делим отрезок от 18 до 22 на 6 частей

1 часть - (22-18) : 6 = 4/6 или в клетках - 12:6 = 2 клетки

Середина отрезка - к 18 прибавить половину полученных частей - три из шести или от 22 вычесть 3 части - результат будет одинаков.

18 + 3 * 4/6 = 18+12/6 = 18+2 = 20

22 - 3*4/6 = 22 - 12/6 = 20

2) Делим отрезок от 19 до 20 на 10 частей

1 часть - (20-19)/10 = 1/10.

Середина отрезка - к 19 прибавить 5 по 1/10 или от 20 вычесть 5 по 1/10

19 + 5/10 = 19 1/2

20 - 5/10 = 19 1/2