Решите пожалуйста подробно

Ответы
Разобьем девятиугольник на шестиугольники.
Если точки A и C лежат на окружности PQO, то мы легко возьмем на дуге AC точку B, поэтому ее положение, а также положение точек E и H, нас не интересует.
Пусть все три шестиугольника вписанные.
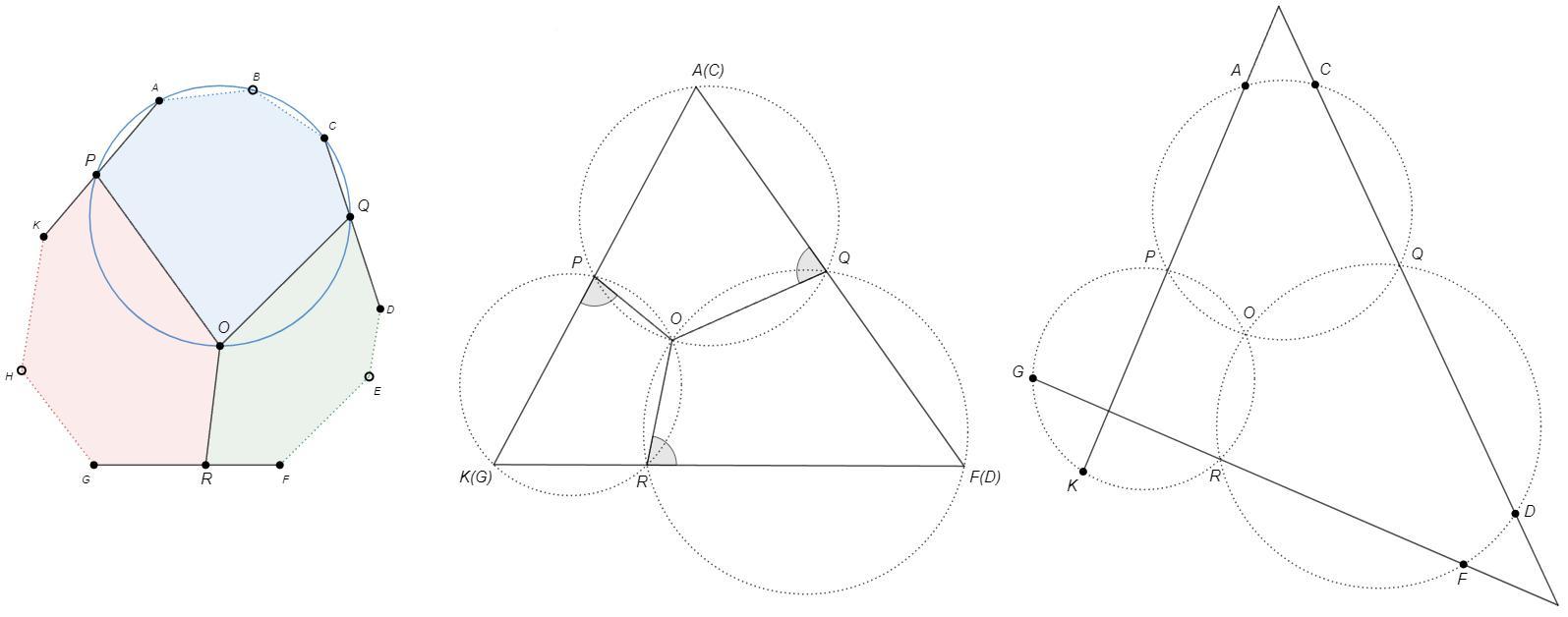
Тогда имеем три окружности с общей точкой O и хордами PO QO RO.
Совместим точки A-C и D-F. По теореме о внешнем угле вписанного четырехугольника ∠KPO=∠AQO=∠FRO => KPOR - вписанный, т.е. прямые AP и FR пересекутся на окружности POR. Cчитаем, что это совместились точки K-G и образовали треугольник.
Теперь разведем точки A-С. При этом прямые AK и CD должны пересекаться вне окружности, иначе получим девятиугольник с самопересечением. По теореме об угле между секущими ∠(AP;CQ) уменьшится (из половины дуги PQ вычтется половина дуги AC). Аналогично разведем точки D-F, ∠(DQ;FR) уменьшится. Тогда ∠(KP;GR) очевидно увеличится, а значит хорды пересекутся внутри окружности и мы получим девятиугольник с самопересечением.
Это противоречит условию, следовательно все три шестиугольника не могут быть вписанными.