Question

- Написати рівняння площини, яка проходить через т. М (1; - 1; - 1) перпендикулярно до прямой (x + 3)/2 = y - 1/- 3 = z+2/4

- Написать уравнение плоскости, проходящей через т. м (1; - 1; - 1) перпендикулярно прямой (x + 3)/2 = y - 1/- 3 = z+2/4

Answer 1

Ответ:

Уравнение плоскости :   $\bf A(x-x_0)+B(y-y_0)+C(z-z_0)=0$  , где

$\bf \overline{n}=(A,B,C)$  -  нормальный вектор плоскости , который ортогонален

(перпендикулярен) этой плоскости ,   $\bf M_0(x_0,y_0,z_0)$ - точка на плос-

кости .

Уравнение прямой в пространстве :  $\bf \dfrac{x-x_0}{m}=\dfrac{y-y_0}{n}=\dfrac{z-z_0}{p}$   ,

где  $\bf \overline{s}=(m,n,p)$ - направляющий вектор прямой, который колли-

неарен  (параллелен) этой прямой ,  $\bf M_0(x_0,y_0,z_0)$ - точка на прямой .

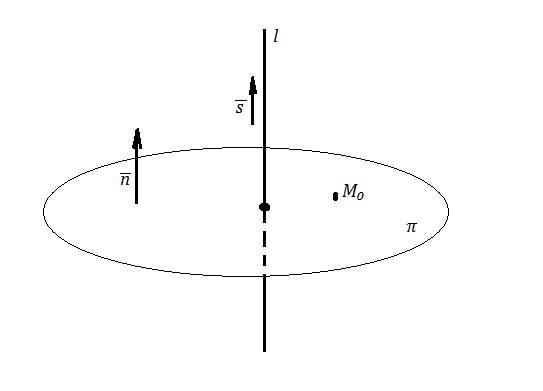
 Если прямая перпендикулярна плоскости , то направляющий вектор прямой   $\bf \overline{s}=(m,n,p)$  , будет перпендикулярен плоскости . Значит он может служить нормальным вектор плоскости ,  $\bf \overline{s}=\overline{n}$  .

Если плоскость перпендикулярна прямой , то нормальный вектор плоскости   $\bf \overline{n}=(A,B,C)$  параллелен этой прямой . Значит нормальным вектором плоскости может служить направляющий вектором прямой ,  $\bf \overline{n}=\overline{s}$  .

$\bf \dfrac{x+3}{2}=\dfrac{y-1}{-3}=\dfrac{z+2}{4}\ \ \ \Rightarrow \ \ \ \overline{s}=(\, 2\, ;-3\, ;\, 4\, )=\overline{n}\\\\\\M(\ 1\, ;-1\, ;-1\, )\ \ \ \Rightarrow \ \ \ 2\, (x-1)-3\, (y+1)+4\, (z+1)=0\ \ ,\\\\\boldsymbol{\pi :\ 2x-3y+4z-1=0}$