Предмет: Алгебра,
автор: Mykola988
Доведіть тотожність:
Приложения:
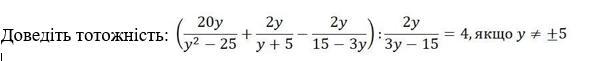
Ответы
Автор ответа:
1
Ответ:
Объяснение:
Mykola988:
ем я только что решил сам
Похожие вопросы
Предмет: Русский язык,
автор: 1basaraevi
Предмет: Математика,
автор: dehtarenkoegor
Предмет: Українська мова,
автор: vynyarchuklarysa
Предмет: Английский язык,
автор: ariamanson