Предмет: Алгебра,
автор: neta9479
sqrt((x + 3)/(x - 3)) - 6sqrt((x - 3)/(x + 3)) + 1 = 0
Помогите, пожалуйста
Приложения:
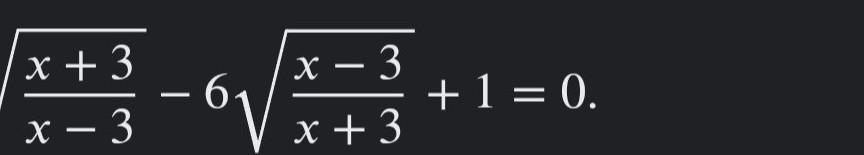
Ответы
Автор ответа:
2
Ответ:
Решить уравнение . Метод замены .
Замена:
Возвращаемся к старой переменной .
не подходит
Проверка .
Ответ: .
Приложения:

neta9479:
спасибо большое
Похожие вопросы