1.Знайдіть відстань від точки M(- 3; -2) до точки N(4; - 4) .
2.Серед векторів a(- 2; 4) ,
b (2;2), c (0;-1), d (1;-2) знайдіть колінеарні.
Будь ласочка допоможіть
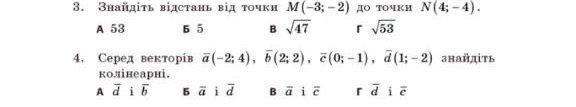
Ответы
Ответ:
1. Щоб знайти відстань між точками M(-3; -2) та N(4; -4), використовуйте формулу відстані між двома точками у площині:
Відстань = √((x₂ - x₁)² + (y₂ - y₁)²)
В нашому випадку:
x₁ = -3, y₁ = -2
x₂ = 4, y₂ = -4
Відстань = √((4 - (-3))² + (-4 - (-2))²)
Відстань = √(7² + (-2)²)
Відстань = √(49 + 4)
Відстань = √53
Відстань між точками M і N дорівнює √53.
2. Щоб визначити, які вектори серед a, b, c, і d є колінеарними, перевіримо, чи їхня кількісна характеристика співпадає. Вектори колінеарні, якщо один можна отримати, множивши інший на деяке число.
a(-2; 4)
b(2; 2)
c(0; -1)
d(1; -2)
Для перевірки колінеарності давайте порівняємо вектори за допомогою їхніх компонентів:
a/b = (-2/2; 4/2) = (-1; 2)
b/c = (2/0; 2/(-1)) - не визначено (оскільки не можна ділити на нуль)
c/d = (0/1; (-1)/(-2)) = (0; 1/2)
a/d = (-2/1; 4/(-2)) = (-2; -2)
З отриманих відношень видно, що вектори a і d є колінеарними, оскільки один можна отримати, помноживши інший на -1.