Предмет: Алгебра,
автор: iMich
Розв’яжіть нерівність
2Log(2)/(5)+\log _(5)x-3<=0 Допоможіть будь ласка
Приложения:
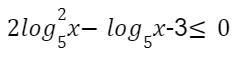
Ответы
Автор ответа:
0
Ответ:
Объяснение:
замінюємо
Похожие вопросы
Предмет: Українська мова,
автор: evgeniadubovik1
Предмет: Биология,
автор: polisar1102
Предмет: Алгебра,
автор: afgfg3019
Предмет: Английский язык,
автор: dsd2wdfefasdff
Предмет: Алгебра,
автор: JUST1ILYA