Предмет: Геометрия,
автор: kkyrovska
В правильной шестиугольной пирамиде высота равна h, а боковая грань пирамиды образует с основанием угол y. Найдите площадь полной поверхности пирамиды.даю 30 балов
kkyrovska:
это да.... я с этими задачами второй день сижу
спасибо)
Ответы
Автор ответа:
1
Ответ:
Sп=2h²√3(tgγ+sinγ)/(tg²γ*sinγ);
Объяснение:
sinγ=SO/SH; →
SH=SO/sinγ=h/sinγ;
tgγ=SO/OH; →
OH=SO/tgγ=h/tgγ;
∆COD- равносторонний треугольник.
OH=CD√3/2; - высота равностороннего треугольника. →
СD=2*OH/√3=(2/√3)*(h/tgγ)=
=2h/(tgγ*√3);
Sб=½*6*СD*SH=3*2h/(tgγ*√3)*h/sinγ=
=3*2h*h/(√3*tgγ*sinγ)=
=2h²√3/(tgγ*sinγ);
So=6*CD²√3/4=3√3/2*(2h/(√3*tgγ))²=
=3√3/2*4h²/3tg²γ=
=2h²√3/tg²γ;
Sп=Sо+Sб=
=2h²√3/tg²γ+2h²√3/(tgγ*sinγ)=
=((2h²*√3*tgγ)+(2h²*√3*sinγ)/(tg²γ*sinγ)=
=2h²√3(tgγ+sinγ)/(tg²γ*sinγ);
Приложения:
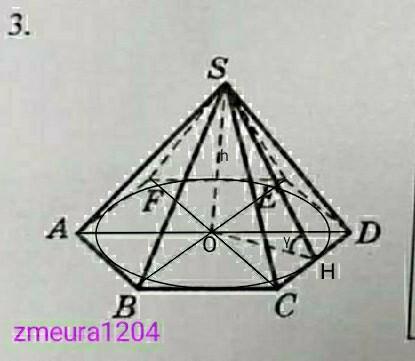
спасибо большое!!
Будь ласка.
Похожие вопросы
Предмет: Английский язык,
автор: annavolosiuk00
Предмет: Математика,
автор: AEIXWNM
Предмет: Українська мова,
автор: Wert2012
Предмет: Математика,
автор: icon3
Предмет: Алгебра,
автор: kanykey07