Question

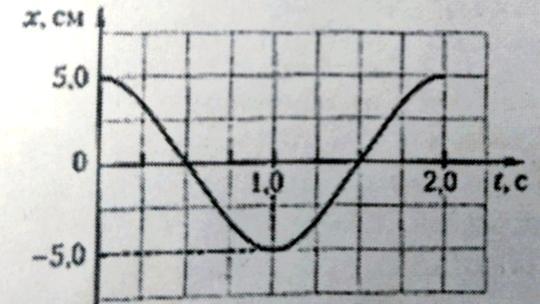
Дан график зависимости проекции смещения шарика массой 40 г, подвешенного на невесомой пружине, от времени. Найти модуль максимального импульса шарика.

Answer 1

Объяснение:

Перед нами график гармонических колебаний (если точнее — косинусоида). Её уравнение выглядит следующим образом:

$x(t) = x_m \cos( \omega t)$

где x_m — амплитуда, ω — циклическая частота

Импульс есть произведение массы на скорость, а скорость, как известно, это первая производная перемещения

$v(t)= x_m \omega \sin( \omega t)$

Минус не учитываем, так как в задаче просят найти модуль.

$p(t)= x_m m \omega \sin( \omega t)$

значение будет максимальным, когда sin = 1

Учтём, что

$\omega = \frac{2\pi}{T}$

За один период точка проходит 4 амплитуды

Значит период этой функции — 2с.

Итого:

$p_m = \frac{2mx_m\pi}{T}$

$p_m = \frac{2 \times 0.04 \times 0.05\pi}{2}$

$p_m =0.002\pi$