Предмет: Алгебра,
автор: ilizilidfjj2006
Допоможіть будь ласка 50 балів
Приложения:
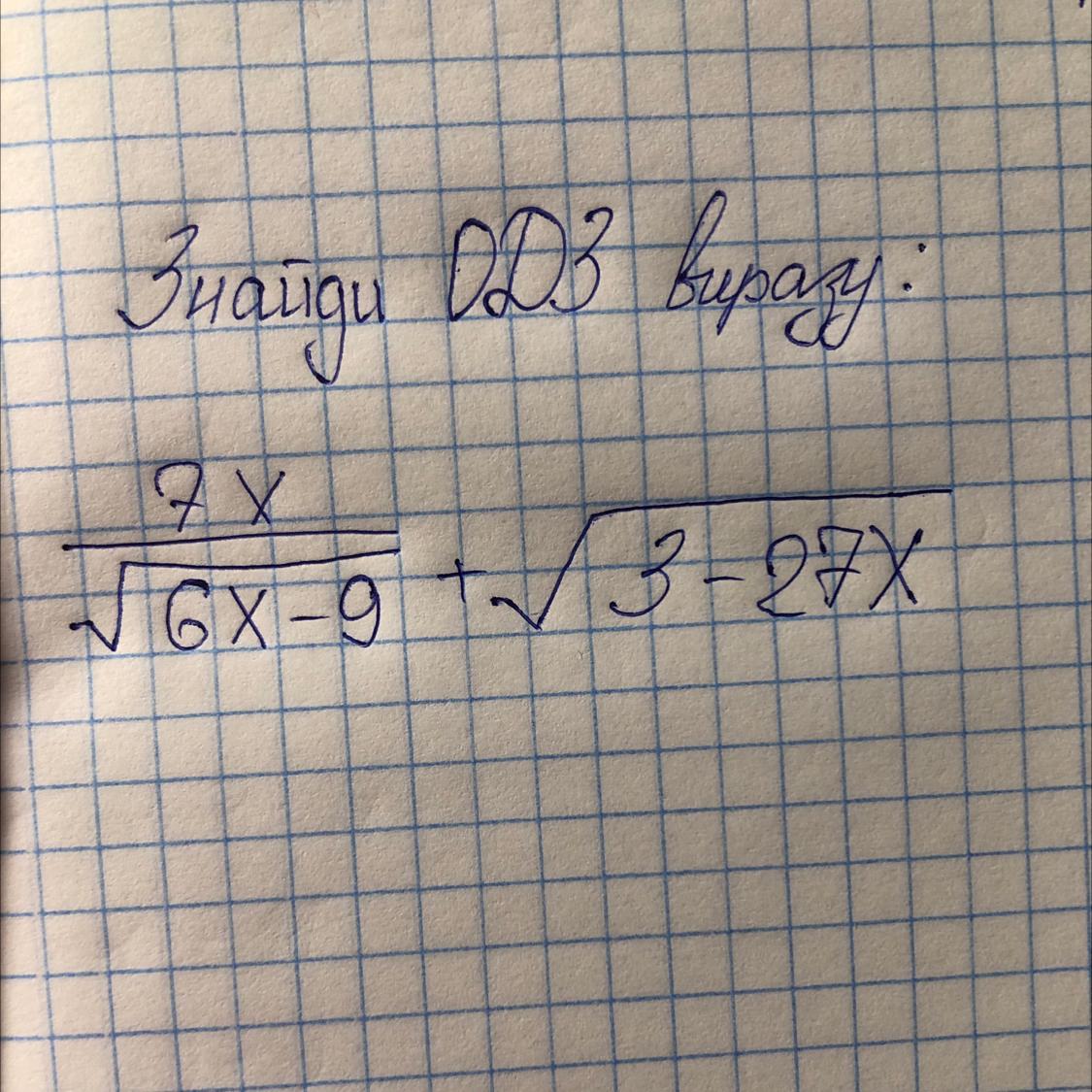
Ответы
Автор ответа:
0
Ответ:
Найти ОДЗ выражения .
Знаменатель дроби не может быть равен 0 . Подкоренное выражение корня чётной степени - неотрицательно .
Получили два непересекающихся множества . Значит решений система не имеет .
Ответ: .
Приложения:

Похожие вопросы
Предмет: Українська література,
автор: hmelnickaaroslava0
Предмет: Английский язык,
автор: pvlad3349
Предмет: Математика,
автор: Аноним
Предмет: Математика,
автор: zeynalovrasad9
Предмет: Химия,
автор: vindaha2004